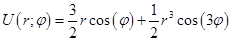4. Решить задачу Дирихле для уравнения Лапласа в круге

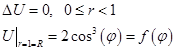
Решение:
Общая формула решения задачи Дирихле в круге имеет вид:
,
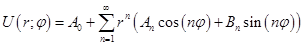где коэффициенты 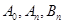вычисляются по формулам для вычисления коэффициентов ряда Фурье: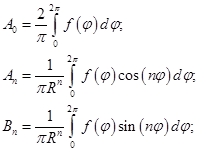

Однако в этой задаче граничное условие можно представить в виде суммы синусов и косинусов, и вычислять интегралы не требуется, достаточно лишь приравнять коэффициенты при одинаковых функциях.
Преобразуем граничное условие по тригонометрическим формулам:

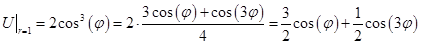
Подставим в выражение для :

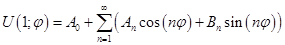
Используем граничное условие:

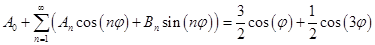
Распишем суммы для большей наглядности:

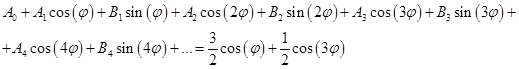
Приравняем коэффициенты при одинаковых функциях в правой и левой частях равенства. Заметим, что синусов в правой части вообще нет, т.е. 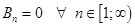, а косинусы есть только для 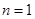и .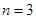
Получили, что 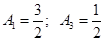, а все остальные коэффициенты равны нулю. Поставим эти коэффициенты в выражение для: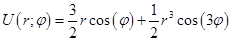
— это и есть искомая функция.
Ответ: