Одно из задач по теории логистики является задача по определению оптимального месторасположения распределительного центра при заданных координатах клиентов и поставщиков, а также заданных тарифах на перевозку и объемах поставок.
Формула имеет вид:

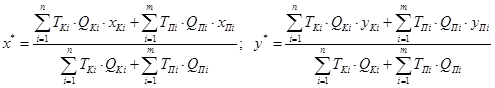
, где 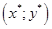— координаты распределительного центра (искомые),
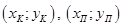— координаты Клиентов и Потребителей соответственно,
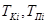— тарифы на перевозку груза для Клиентов и Поставщиков,
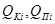— объемы груза, реализуемые или потребляемые Клиентами и Поставщиками.

Пример решения задачи по определению оптимального места расположения распределительного центра.

Задача:
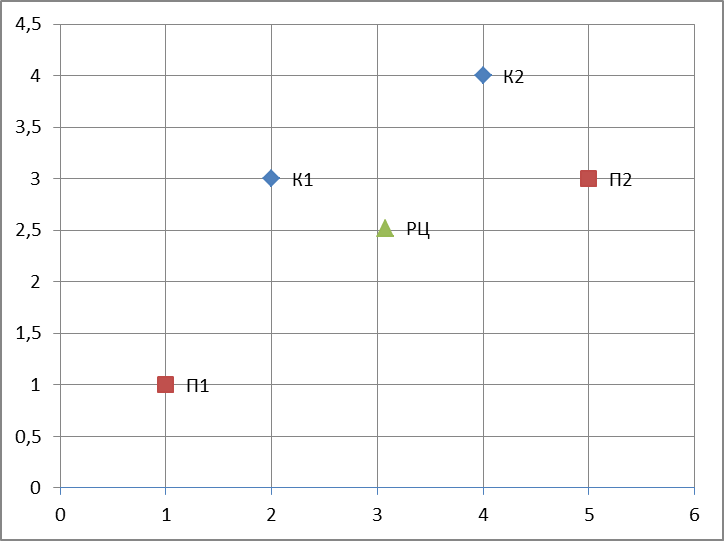
На карте местности точками обозначены поставщики ( 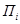) и клиенты-потребители ( ).

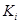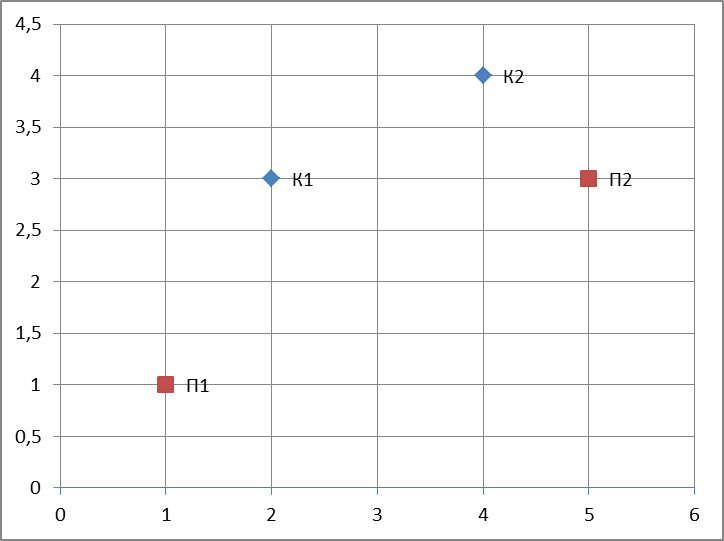
Рассчитать координаты распределительного центра так, чтобы совокупные расходы на транспортировку были минимальны.
Расходы на транспортировку (руб. на т за км) и объем партий (т) заданы в виде таблице.

	Поставщики		Клиенты-потребители
	П1	П2	К1	К2
T	3	2	1	2
Q	150	200	100	150

Решение:
Расширим таблицу данных, внеся в нее координаты объектов.

	Поставщики		Клиенты-потребители
	П1	П2	К1	К2
Х	1	5	2	4
Y	1	3	3	4
T	3	2	1	2
Q	150	200	100	150

Найдем абсциссу расположения распределительного центра

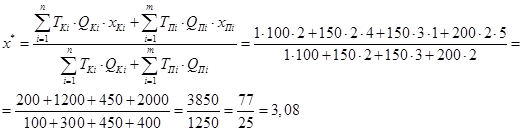
Найдем ординату расположения распределительного центра

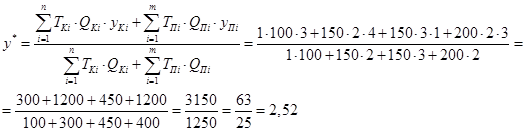
Ответ: Координаты распределительного центра : 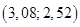. Отметим его расположение на карте: