Рассмотрим пример отделения корней многочлена по методу Штурма на примере многочлена .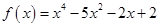
Для применения этого метода к многочлену 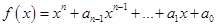требуется составить систему Штурма .
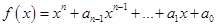Замечание: многочлен 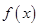должен иметь действительные коэффициенты и не иметь кратных корней.
Правило построение системы Штурма:
1)
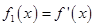
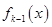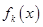2) Если известны и , то 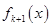будет равен остатку от деления 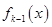на 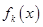, взятым с обратным знаком:
.
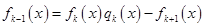Замечание: В процессе деления, в отличии от алгоритма Евклида, остаток можно умножать лишь на произвольное положительное число (для того, чтобы коэффициент при старшей степени был целым или просто удобным), т.к. знак остатка принципиально важен.
Составим систему Штурма для заданного многочлена
1)
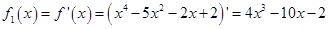
2)

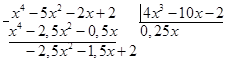
Умножаем остаток на 4 и берем его с противоположным знаком.
Получим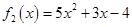
3)

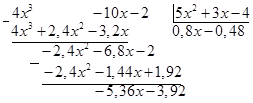
Домножим на 25, поменяем знак и получим: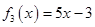
4)

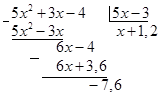
Домножим остаток на обратную величину, поменяем знак и получим: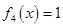
Получили систему Штурма:

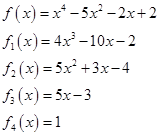
Определим знаки этих многочленов 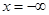при и при 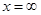. Конечно, вычислять тут ничего не нужно, достаточно посмотреть только на коэффициенты при старших степенях и на сами эти степени. Например:

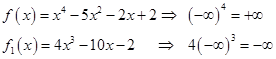
И т.д. Занесем результаты выводов в таблицу:

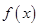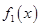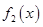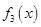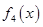						Кол-во перемен знаков
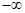	+	—	+	—	+	4
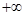	+	+	+	+	+	0

Вывод: Многочлен имеет ровно 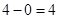действительных корня.
Локализуем их. Для этого продолжим таблицы, выбрав «на глазок» точки для проверки знаков многочленов системы. Первую точку нужно взять такой, чтобы набор плюсов и минусов был одинаков с 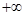, а последующие выгодны такие, при которых количество перемен знаков изменяется, причем таких перемен должно быть ровно столько, сколько корней имеет многочлен.

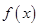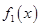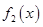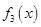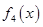						Кол-во перемен знаков
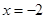	+	—	+	—	+	4
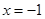	0	+	—	—	+	2

Замечание: повезло, т.к. при 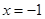получаем 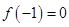, т.е. 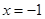— корень многочлена. Мы не только локализовали, но определили его точное значение. Заметим, что количество перемен знаков уменьшается на 2, т.е. на этом интервале есть один корень, он дает одно изменение, и корень в этой точке дает еще одну перемену. Но продолжим.

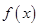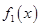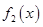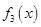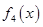						Кол-во перемен знаков
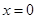	+	—	—	—	+	2
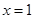	—	—	+	+	+	1
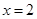	—	+	+	+	+	1
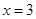	+	+	+	+	+	0

Вывод: Про корни можно сказать: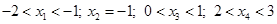
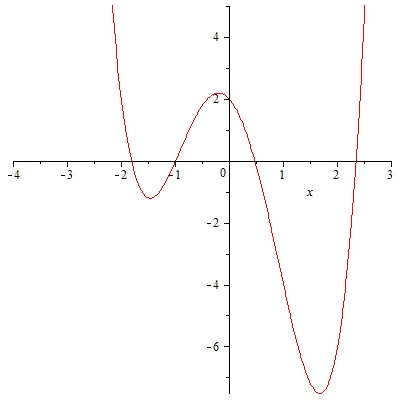
При помощи компьютерных технологий можно построить график функции 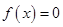и убедиться в правильности рассуждений.