Задача: Функция полезности потребителя двух товаров, приобретаемых в количестве X и Y соответственно, имеет вид .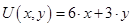

При каком минимальном доходе покупатель может извлечь из покупки полезность, равную 150 ед., если цены на товары соответственно равны 2 и 5 ден. ед.

Решение:

Пусть М – доход покупателя, тогда, учитывая стоимость товаров, можно записать целевую функцию: .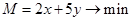

Учитывая, что полезность должна составить 150 ед., вводим условие: .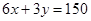

Далее переходим к графической интерпретации задачи на координатной плоскости XOY, где допустимое множество решений представляет собой отрезок прямой

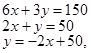
заключенный в первой координатной четверти, из соображений, что .

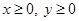На этом же графике построим целевую функцию

,
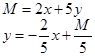где M – произвольная константа.

Эта прямая, т.к. задача решается на минимум, должна занять самое низкое положение из всех возможных, при которых она будет пересекать прямую-ограничение .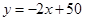

Для определенности, будем считать 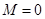, построим график функции 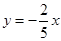(пунктир) и проанализируем его положение, удовлетворяющее требованиям задачи.

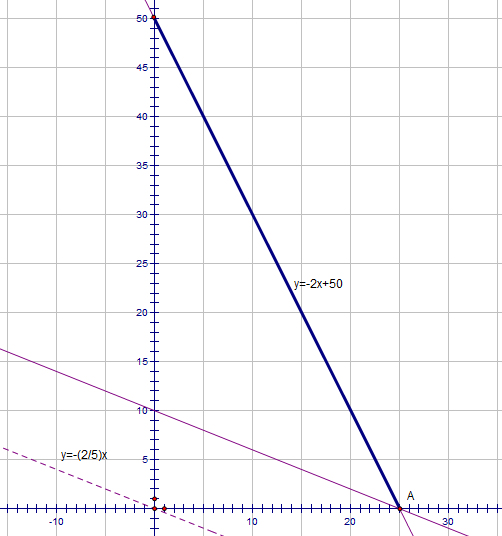
Получили, что к решению задачи приводит положение прямой, проходящее через точку А(0;25).
Найдем значение параметра М, при котором это происходит:

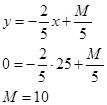
Ответ: Покупатель извлечет из покупки полезность, равную 150 ед. при минимальном доходе 10 единиц.