Этот курс рассчитан на самостоятельную подготовку к экзаменам по математике в средней школе. Курс будет постоянно пополняться уроками, в каждом из которых будут задачи для самостоятельного решения, с ответами или с полными решениями. Курс рассчитан для подготовки школьников от А до Я.

Урок 1.

Целые числа.

Самыми простыми для понимая числами являются те числа, которые мы используем для счета предметов. Например, один стул, два стула, тридцать восемь попугаем. Это целые и положительные числа. Все такие числа, целые положительные и ноль, называются натуральными числами. Арифметические операции, т.е. сложение, вычитание, умножение и деление, с натуральными числа просты, интуитивно понятны и доступны для вычисления на счетных палочках или пальцах.

Примеры:

Таблицу умножения выучить обязательно.
Таблица умножения:

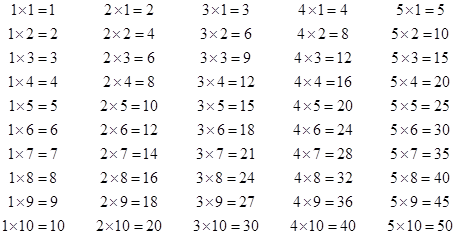
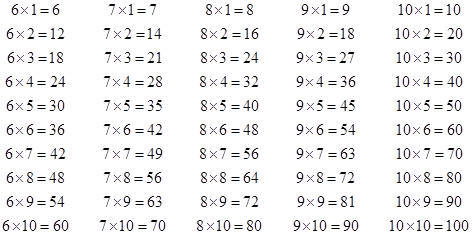
Порядок действий.

«Умножение» и «деление» имеет более высокий приоритет, чем «сложение» и «вычитание», т.е. выполняются первыми.
Пример:

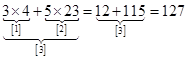
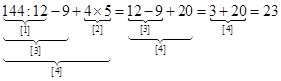
От перестановки слагаемых местами сумма не изменяется. От перемены сомножителей местами произведение не изменяется.
Пример:

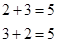
и

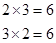
Отрицательные числа.

Конечно, читатель уже знает, что кроме положительных чисел существуют и отрицательные. Проще всего их понять, да и исторически они возникли на примере денежного долга. Если вы имеете пустые карманы и при этом должны кому-нибудь, к примеру, 5 рублей, то вас баланс составляет минус 5 рублей.

Вычитание из большего меньшего.

Здесь проблем быть не может:

.

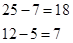Вычитание из положительного числа.

Вычитание из меньшего большего.

Правило: Для того, чтобы вычислить разность между меньшим и большим числом, нужно из большего вычесть меньшее, и у результата поменять знак.

Например, требуется вычислить разность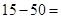
15 меньше, чем 50, поэтому берем большее число, т.е. 50, вычитаем из него меньшее, т.е. 15, получаем 35, и меняем знак. Получим, что .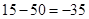

Еще один пример:
Требуется вычислить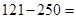
Из меньшего вычитается большее, поступаем по алгоритму, вычитаем из большего меньшее: 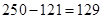и у результата меняем знак, получим .

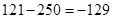Задания для самостоятельного решения:
№ 1.1

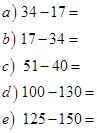
Ответы:

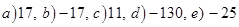
Сложение отрицательного и положительного числа.

Например, требуется вычислить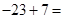
Вспоминаем, что от перестановки мест слагаемых (а вычитание и сложение по сути одно и то же) сумма не меняется и переставляем слагаемые:

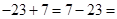
Получаем вычитание из меньшего большего, действуем по схеме, изложенной выше, т.е. вычитаем из большего меньшее: 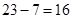и меняем знак, получим: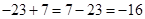

Вычитание из отрицательного числа другого отрицательного:

Например, требуется вычислить: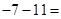
Есть два числа, -7 и -11, возьмем такие же, но без минуса, т.е. 7 и 11, найдем их сумму: 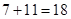, и припишем минус, получим: .

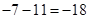Попробуем еще раз: Вычислите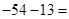
Берем числа без минусов, 54 и 13, вычисляем их сумму 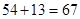, меняем знак:
.

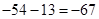Задания для самостоятельного решения:
№ 1.2

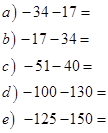
Ответы:

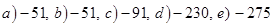
Применение числовой оси для сложения и вычитания чисел любого знака.
Отличной визуализацией при работе с числами служит числовая ось. Это направленная прямая, на которую нанесены метки, соответствующие числам. Чем правее метка, тем больше число, и чем левее – тем меньше. Чаще всего в середине отмечают 0.