Метод Феррари — аналитический метод решения алгебраического уравнения четвёртой степени.
Формулы для решения уравнений третьей степени дал нам Джероламо Кардано, а его ученик оказался не менее талантлив, и рассказал нам как решать уравнение четвертой степени. Оба алгоритма Кардано опубликовал в своей книге «Высокое искусство». Рассмотрим метод Феррари на примере.
Задача: решить уравнение: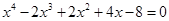
Решение:
Общий вид :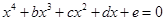

1) Сделаем замену: . С помощью нее должно получиться уравнение вида: (*)

Сделаем это.
Замена: .

После раскрытия скобок и приведения подобных получим:
(*), т.е.

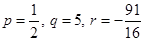
2) Составим уравнение вида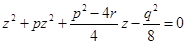
, от этого уравнения нужен лишь один его корень 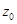( если , то это уравнение всегда имеет положительный корень).
Получим:

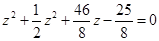
Подберем корень, как – неважно. Здесь нам было откровение, корень этого уравнения ( проверить это можно банальной подстановкой).
3) Корни уравнений (*) определим из уравнений:

Решим первое:

Решим второе:

Итого, корни уравнений (*):
;

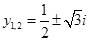4) Сделаем обратную замену:
, т.е.
;

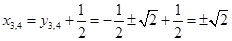
Ответ: 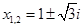;