Дано интегральное уравнение Вольтерра:
(*)
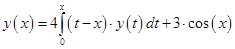Решение:
Дважды продифференцируем это уравнение:
(**)
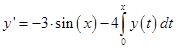И еще разок:

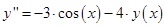
Получили обыкновенное дифференциальное уравнение первой степени с постоянными коэффициентами, запишем в каноническом виде:

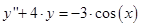
Начальные условия определим из (*) и (**)

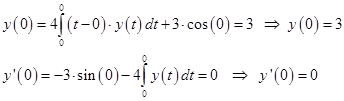
Итого, решим уравнение

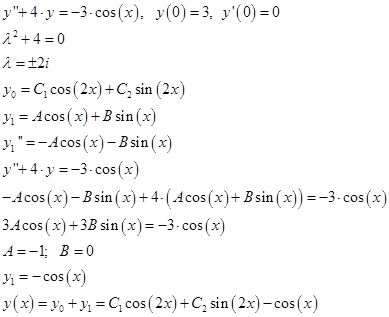
Определим константы из начальных условий:

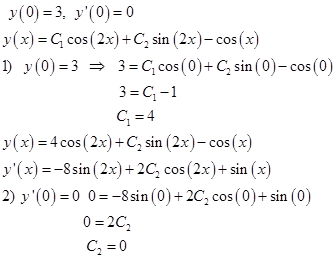
Ответом в этом интегральном уравнении будет функция