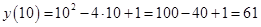В этой задаче дан график, дана функция в общем виде или с частично определенными коэффициентами, и требуется найти, например, значение функции в какой-то точке.
Графики бывают: прямая, парабола, гипербола, логарифм, показательная.
Начнем с линейной функции.

Линейная функция.

Задача.
Дан график, на котором изображены две прямые. Требуется определить абсциссу точки пересечения этих прямых.

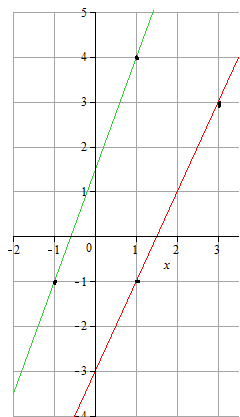
Решение:
Общий вид уравнения прямой 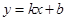. И по-хорошему нам бы составить эти уравнения для обеих прямых, т.е. определить их соответствующие коэффициенты. В уравнении каждой прямой два параметра, и на каждой прямой даны нам по две точки.
НО! Мы же понимаем, что а задаче будут более или менее нормальные коэффициенты, поэтому для красной прямой мы можем немного схитрить. Достаточно четко видно, что она пересекает ось ординат в точке с координатой -3, т.е. .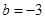

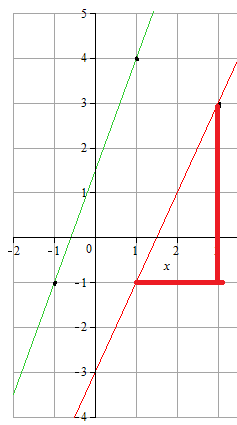
А для определения углового коэффициента построим треугольник с вершинами в данных точках и поделим вертикальный катет на горизонтальный.
.
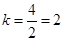Всё, мы определили уравнение красной прямой: .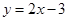
С зеленой прямой поступим стандартно, она проходит через точки с координатами 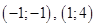, подставим их в общий вид уравнения прямой вместо соответствующих координат и получим систему:

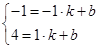
Решив систему получим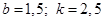
И уравнение этой прямой будет .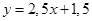
Готово. Остается найти точку пересечения прямых 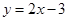и .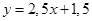

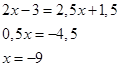
Это и будет абсцисса точки пересечения прямых.
Ответ: -9

Парабола.

Задача.
Дан график функции 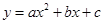. Найти значение .

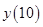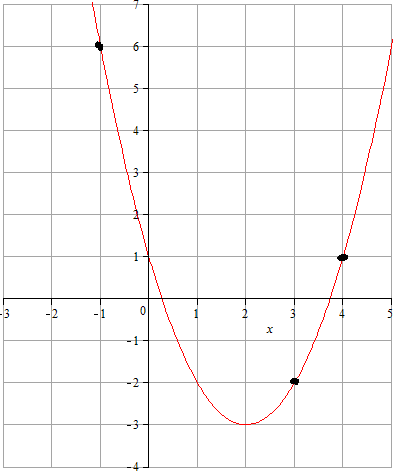
Решение:

Способ первый

, для удачных графиков.
Мы знаем, что парабола пересекает ось ординат в точке 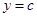, и по графику сразу видим, что .
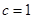Функция стала немножечко понятней: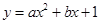
Смотрим дальше. Если из вершины параболы пойти вправо на 1 клеточку и вверх на одну клеточку, то попадем опять на параболу, а если на две клеточки вправо, то вверх на четыре.

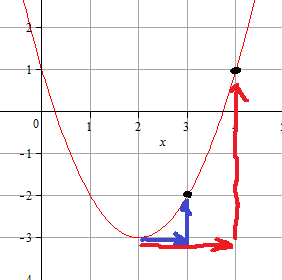
О чем нам это говорит? О том, что это обычная человеческая парабола без растяжений. Т.е.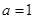
Функция стала еще понятнее: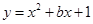
Осталось определить 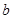из формулы для абсциссы вершины .
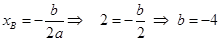Всё, функцию определили: .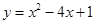
И ответим на вопрос задачи: