Оглавление.
1. Нахождение максимума и минимума функции одной переменной.
2. Нахождение наибольшего и наименьшего значения функции на отрезке.
Один из типов задач математического анализа: исследовать функцию одной переменной на минимум и (или) максимум. Иногда экстремум (собирательное название для минимума и максимума) функции требуется найти на некотором интервале. Задачи подобного плана попадаются также в курсе средней школы и среди заданий Единого Государственного Экзамена.
Постановка задачи 1:
Дана функция 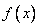 , определенная на некотором промежутке. Требуется найти точки максимумов (минимумов) функции.
, определенная на некотором промежутке. Требуется найти точки максимумов (минимумов) функции.
Теоретические основы.
Определение: Говорят, что функция 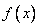 имеет в точке
имеет в точке 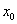 максимум , рис. а) ( или минимум, рис. б) ) , если существует некоторая окрестность
максимум , рис. а) ( или минимум, рис. б) ) , если существует некоторая окрестность 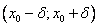 в промежутке, где функция определена, что для всех точек этой окрестности выполняется неравенство
в промежутке, где функция определена, что для всех точек этой окрестности выполняется неравенство
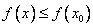 (
( 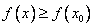 ).
).
Замечание:
Extremum- (латынь) крайнее.
Maximum – (латынь) наибольшее.
Minimum – (латынь) наименьшее.
Необходимое условие экстремума (Теорема Ферма):
Пусть функция 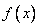 определена на некотором промежутке и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная
определена на некотором промежутке и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная 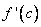 , то необходимо
, то необходимо 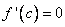 .
.
Определение: Если выполняется равенство 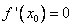 , то точку
, то точку 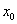 будем называть стационарной точкой.
будем называть стационарной точкой.
Определение: Стационарные точки и точки, в которых не существует двусторонней конечной производной, будем называть точками, подозрительными на экстремум.
Иллюстрация некоторых случаев, кроме представленных выше двух:
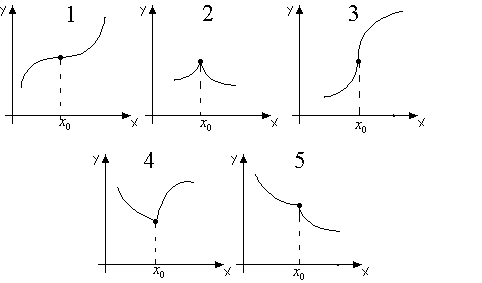
1) Экстремума нет, первая производная равна нулю.
2) Точка максимума, первая производная слева и справа бесконечна.
3) Экстремума нет, первая производная слева и справа бесконечна.
4) Точка минимума, первая производная слева не равна первой производной справа.
5) Экстремума нет, первая производная слева не равна первой производной справа.
Замечание (Геометрический смысл производной):
Производная функции 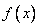 в точке
в точке  численно равна угловому коэффициенту касательной к графику функции
численно равна угловому коэффициенту касательной к графику функции  , проведенной в точке
, проведенной в точке 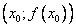 .
.
Пример 1:
Рассмотрим функцию 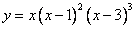 .
.
Вычислим производную этой функции:

Итак, точки, подозрительные на экстремум: 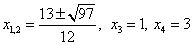
Построим график этой функции.

На графики видно, что функция имеет максимум при 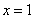 , минимумы при
, минимумы при 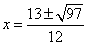 . При
. При 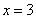 функция экстремума не имеет.
функция экстремума не имеет.
Из этого примера видно, что равенство нулю производной в точке является обязательным условием экстремума функции в этой точке, но не является достаточным условием.
Теорема (условие монотонности функции):
Пусть функция 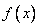 определена и непрерывна в непрерывна в некотором промежутке и внутри него имеет конечную производную
определена и непрерывна в непрерывна в некотором промежутке и внутри него имеет конечную производную 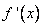 . Для того, чтобы
. Для того, чтобы 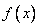 была на этом промежутке монотонно возрастающей (убывающей) в широком смысле, необходимо и достаточно условие
была на этом промежутке монотонно возрастающей (убывающей) в широком смысле, необходимо и достаточно условие
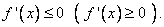
Достаточное условие экстремума:
Предположим, что в некоторой окрестности 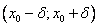 стационарной точки
стационарной точки 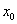 существует конечная производная
существует конечная производная 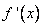 и как слева от
и как слева от 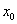 ,так и справа от
,так и справа от 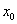 ( в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:
( в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:
1) 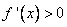 при
при 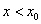 и
и 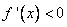 при
при 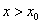 (производная
(производная 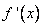 при переходе через точку
при переходе через точку 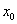 меняет свой знак с плюса на минус). Т.е. при
меняет свой знак с плюса на минус). Т.е. при 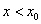 функция возрастает, а при
функция возрастает, а при 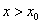 — убывает. Значит, значение
— убывает. Значит, значение 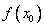 будет наибольшим в промежутке
будет наибольшим в промежутке 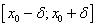 . Другими словами, в точке
. Другими словами, в точке 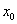 функция имеет максимум.
функция имеет максимум.
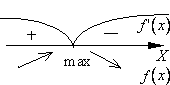
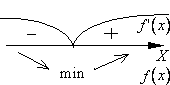
Пояснение: Сверху от числовой оси указывается знак производной на соответствующем интервале, снизу от числовой оси обозначается поведение функции на соответствующем интервале (убывание или возрастание).
2) 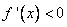 при
при 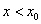 и
и 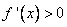 при
при 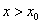 (производная
(производная 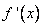 при переходе через точку
при переходе через точку 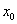 меняет свой знак с минуса на плюс). Т.е. при
меняет свой знак с минуса на плюс). Т.е. при 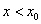 функция
функция 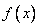 убывает, а при
убывает, а при 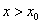 — возрастает. Значит, значение
— возрастает. Значит, значение 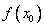 будет наименьшим в промежутке
будет наименьшим в промежутке 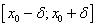 . Другими словами, в точке
. Другими словами, в точке 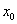 функция имеет минимум.
функция имеет минимум.
3) 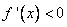 при
при 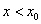 и
и 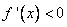 при
при 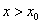 (
( 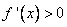 при
при 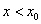 и
и 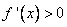 при
при 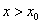 )(производная
)(производная 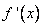 при переходе через точку
при переходе через точку 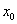 не меняет свой знак). Т.е. функция
не меняет свой знак). Т.е. функция 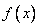 в промежутке
в промежутке 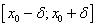 убывает (возрастает). Другими словами, в точке
убывает (возрастает). Другими словами, в точке 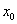 функция
функция 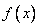 не имеет экстремума.
не имеет экстремума.
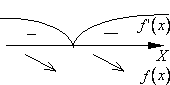
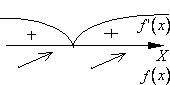
Пример 2:
Рассмотрим вновь функцию 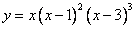 .
.
Производная этой функции имеет вид: 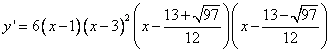
Точки, подозрительные на экстремум: 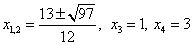 . Выясним знаки производной на соответствующих интервалах (решим методом интервалов неравенства
. Выясним знаки производной на соответствующих интервалах (решим методом интервалов неравенства 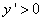 и
и 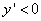 ):
):
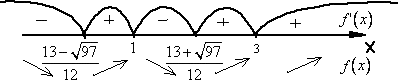
Из рисунка видно, что в точке 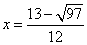 производная меняет свой знак с минуса на плюс, т.е. при
производная меняет свой знак с минуса на плюс, т.е. при 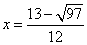 функция имеет минимум.
функция имеет минимум.
В точке 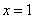 производная меняет свой знак с плюса на минус, т.е. при
производная меняет свой знак с плюса на минус, т.е. при 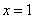 функция имеет максимум.
функция имеет максимум.
В точке 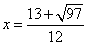 производная меняет свой знак с минуса на плюс, т.е. при
производная меняет свой знак с минуса на плюс, т.е. при 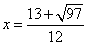 функция имеет минимум.
функция имеет минимум.
В точке 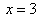 производная своего знака не меняет, т.е. экстремума там нет.
производная своего знака не меняет, т.е. экстремума там нет.
Полученные данные полностью подтверждаются графиком функции.
Алгоритм решения задачи 1.
1) Найти производную функции 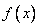 .
.
2) Найти стационарные точки (точки, подозрительные на экстремум), решив уравнение 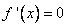 .Обратить внимание на точки, в которых не существует двусторонней конечной производной.
.Обратить внимание на точки, в которых не существует двусторонней конечной производной.
3) Выяснить, меняет ли производная свой знак в точках, подозрительных на экстремум.. Если она меняет знак с минуса на плюс, то в этой точке функция имеет свой минимум. Если с плюса на минус, то максимум, а если знак производной не меняется, то экстремума в этой точке нет.
4) Найти значение функции в точках минимума (максимума).
Дополнение:
Исследование знака первой производной функции по разные стороны от стационарной точки (достаточное условие экстремума) можно заменить исследованием знака второй производной в этой стационарной точке (при условии её существования).
1) если 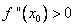 , то функция имеет в этой точке минимум.
, то функция имеет в этой точке минимум.
2) если 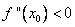 , то функция имеет в этой точке максимум.
, то функция имеет в этой точке максимум.
3) если 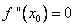 , то вопрос о существовании экстремума в этой точке остается открытым.
, то вопрос о существовании экстремума в этой точке остается открытым.
Пример 3:
Исследовать на экстремум функцию
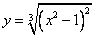
Решение:
1) Найти производную функции 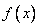 .
.
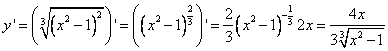
2) Найти стационарные точки (точки, подозрительные на экстремум), решив уравнение 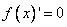 . Обратить внимание на точки, в которых не существует двусторонней конечной производной.
. Обратить внимание на точки, в которых не существует двусторонней конечной производной.
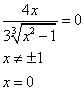
Точки, подозрительные на экстремум: 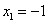 ,
, 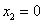 ,
, 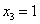 .(т.к. функция в
.(т.к. функция в 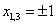 определена)
определена)
3) Выяснить, меняет ли производная свой знак в точках, подозрительных на экстремум. Если она меняет знак с минуса на плюс, то в этой точке функция имеет свой минимум. Если с плюса на минус, то максимум, а если знак производной при переходе через стационарную точку не меняется, то экстремума в этой точке нет.
Решим неравенство 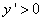 .
.
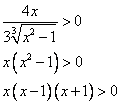
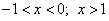
Решим неравенство 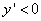 .
.
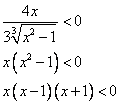
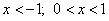
Построим интервалы на числовой оси:
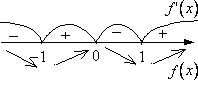
Вывод: при 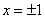 функция имеет минимумы, при
функция имеет минимумы, при 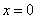 — максимум.
— максимум.
4) Найти значение функции в точках минимума (максимума).
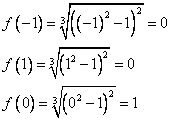
Максимум функции : 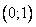 , минимумы:
, минимумы: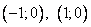 .
.
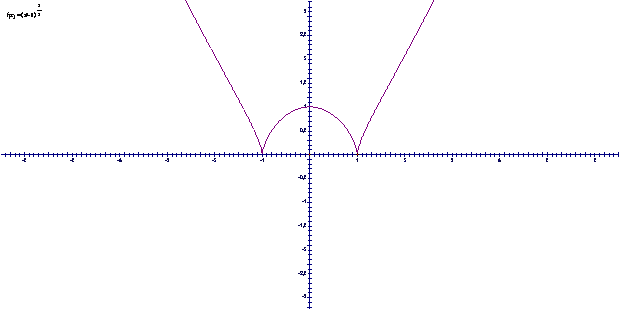
Можно убедиться в правильности полученных результатов взглянув на график этой функции:
Используемая литература:
1) Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления, том 1.


