Оглавление.
1. Нахождение плотности распределения произведения двух независимых случайных величин.
2. Нахождение плотности распределения частного двух независимых случайных величин.
В этой статье рассмотрим достаточно распространенную задачу: нахождение плотности распределения функции двух независимых случайных величин.
Задача:
Найти плотность распределения произведения двух независимых, равномернораспределенных на интервале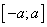 
случайных величин 
.
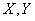Дано: 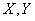— независимы.
, 
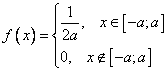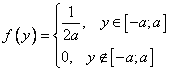
Найти функцию плотности распределения случайной величины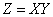 
.
Решение:
Найдем двумерную функцию распределения.
Так как 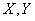— независимы, то 
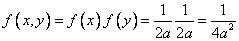при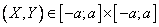 
. Вне этой области = 0.
Найдем закон распределения величины 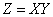. Для этого воспользуемся геометрической интерпретацией функции распределения, аналогичной функции одного аргумента. Но здесь будет уже не кривая а поверхность.
Построим поверхность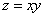 
. Для наглядности тут даны два чертежа.
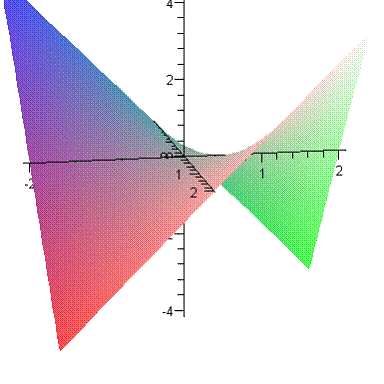
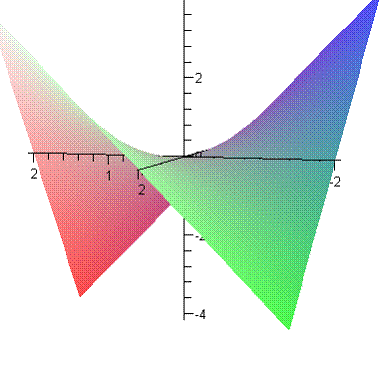
Напомним для одномерного случая:
Значение функции распределения в точке
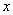равно вероятности того, что случайная величина 
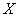примет значения, меньшее 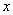, т.е. интересовала область, лежащая левее графика функции распределения.Для двумерного случая интересует вероятность попадания точки ниже поверхности распределения. Рассмотрим какое-то значение
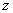. И проведем плоскость, параллельную 
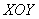. Построим сечение (построим на плоскости 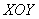кривую, уравнение которой 
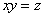) и обозначим область для которой поверхность будет лежать ниже плоскости сечения ( 
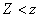). Помним, что распределение идет при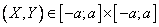 
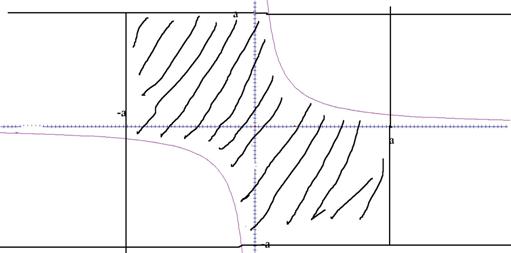
Воспользуемся формулой для функции распределения:
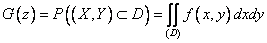
А плотность распределения, соответственно
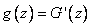
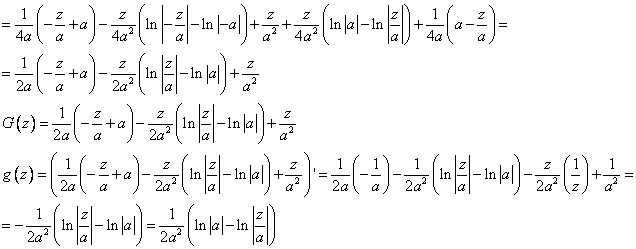
Ответ:
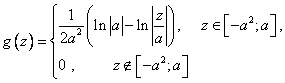
P.S. Статья создана при поддержке одного из читателей сайта.