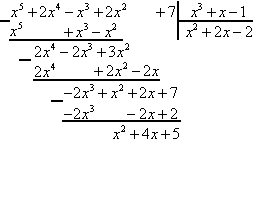Начнем издалека. Когда человек видит перед собой неправильную дробь, то у него возникает непреодолимое желание выделить целую часть. Например, так:
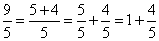
Замечание: Дробь называется неправильной, если числитель больше или равен знаменателю.
Или так, посложнее:
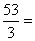
Тут так сразу и не скажешь, придется делить уголком:
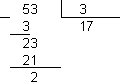
Получили: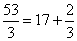 
.
Разберемся с терминологией:
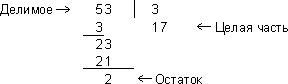
Дроби записываются:
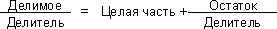
Проведем аналогию на многочлены.
Определение: Дробь, в числителе и знаменателе которой стоят многочлены, называется неправильной, если степень многочлена, стоящего в числителе, больше или равна степени многочлена, стоящего в знаменателе.
Итак, имеется дробь
.
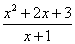Она неправильная, потому что в числителе стоит многочлен второй степени, а в знаменателе – первой, а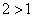 
.
Выделим целую часть:
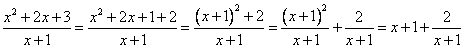
Перечислим участников:
Делимое: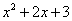 
Делитель: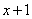 
Целая часть: .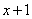
Остаток: 2
Случай сложный, с делением уголком (хотя некоторые говорят «столбиком»)
Требуется выделить целую часть в неправильной дроби:
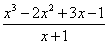
Начнем процесс деления, комментирую происходящее действо:
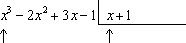
Обращаем внимание только на слагаемые, указанные стрелками.
На что нужно умножить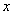 
для того, чтобы получить 
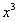? Конечно же на 
.
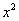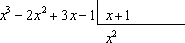
Выполним умножение: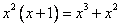 
.
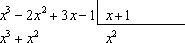
И вычитание из верхнего многочлена нижний, все совсем как при делении уголком чисел.
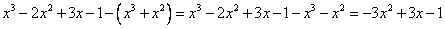
Занесем в «уголок»
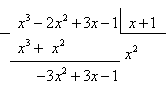
Продолжим. Всегда смотрим на первые слагаемые.
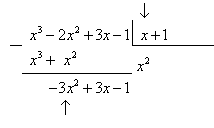
Ответим себе на вопрос: как из 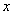можно сделать 
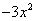? Умножением на 
.
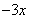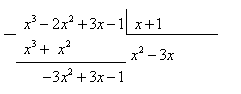
Выполним умножение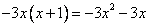 
, занесем в «уголок»
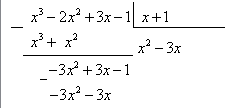
Выполним вычитание:
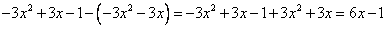
Деление уже примет вид:
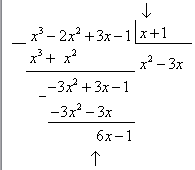
Продолжим. На данный момент нужно из 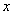получить 
.
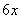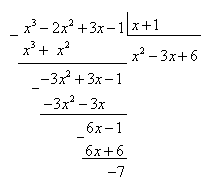
Деление окончено, т.к. из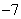 
ну никак не получить .
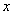Перечислим участников:
Делимое: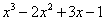 
.
Делитель: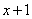
Целая часть: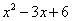 
Остаток: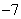
Итог: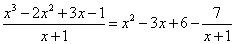 
.
Еще один пример деления, но без комментариев .
Замечание: Обратите внимание на пробелы в записи многочленов. Это сделано для того, чтобы одинаковые степени переменной записывались друг под другом.
