Определение: Общее уравнение кривой второго порядка имеет вид:
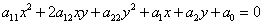 .
.
Основной частью этого уравнения является его квадратичная часть 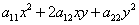 , линейная же часть
, линейная же часть 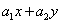 и свободный член уравнения
и свободный член уравнения 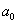 особой роли в приведении к каноническому виду не играют и на общий тип уравнения второго порядка не влияют.
особой роли в приведении к каноническому виду не играют и на общий тип уравнения второго порядка не влияют.
Классификация.
Перечислим все канонические типы уравнений кривых второго порядка:
| П/п | Название | Уравнение | График |
| 1. | Эллипс | 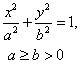 |
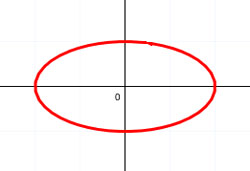 |
| 2. | Мнимый эллипс (пустое множество) | 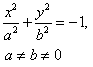 |
|
| 3. | Пара мнимых пересекающихся прямых (точка) | 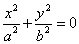 |
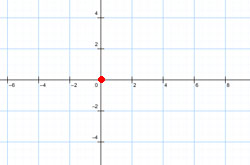 |
| 4. | Гипербола | 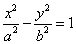 |
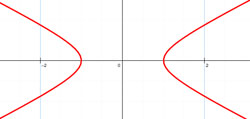 |
| 5. | Пара пересекающихся прямых | 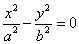 |
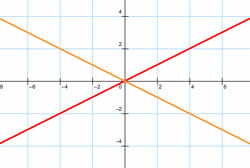 |
| 6. | Парабола | 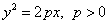 |
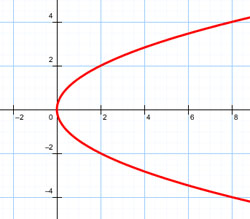 |
| 7. | Пара параллельных прямых | 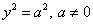 |
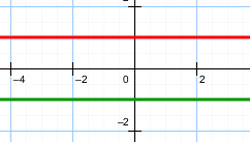 |
| 8. | Пара мнимых параллельных прямых (пустое множество) | 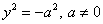 |
|
| 9. | Пара совпадающих прямых | 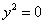 |
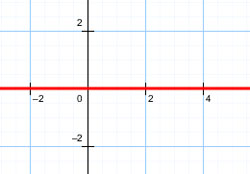 |
Постановка задачи: «Привести к каноническому виду» означает подобрать такие замены для переменных
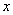 и
и 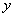 , при которых уравнение
, при которых уравнение 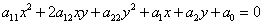 примет один из девяти канонических видов.
примет один из девяти канонических видов.


