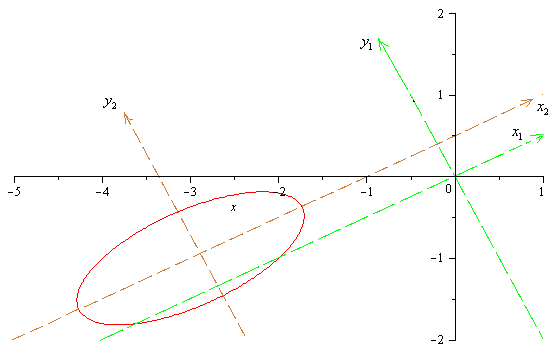
Дано уравнение кривой второго порядка
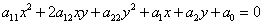. (1)Пример:
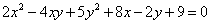
ШАГ ПЕРВЫЙ
Если в уравнении коэффициент
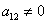, т.е. присутствует слагаемое со смешанным произведением 
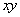, то необходимо перейти к такой системе координат 
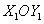, в которой, уравнение (1) после преобразования не содержало бы слагаемое 
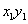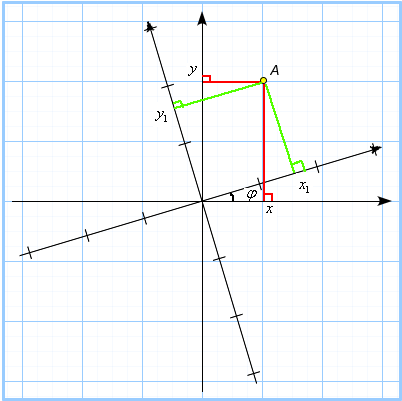
.Это делается при помощи поворота системы координат на некоторый угол
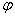, т.е. координаты заменяются по формулам: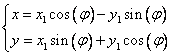
Значение этого угла
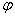можно найти, решив уравнение
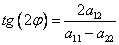,или, оно же в другом виде
.
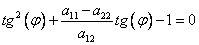Замечание: Как правило, решением тригонометрического уравнения является группу углов, повторяющихся с определенной периодичностью. Для того, чтобы определить угол поворота 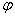для системы координат, следует выбрать любой понравившийся из полученного множества.
Замечание: Предположим, что для решения выбрано первое уравнение, но в исходной записи кривой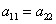 
. Неопытный человек начинает паниковать, т.к. в знаменателе оказывается ноль, а на ноль в школе делить запрещали и т.д. и т.п. Опытный же тригонометривед, знакомый с азами математического анализа и теории пределов вспомнит, что:
.
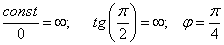Пример:
Выберем корень уравнения с «плюсом»
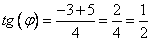
Казалось бы, все хорошо, тангенс угла найден. Но в замене нужны синус и косинус! Что же делать?!!! Следует воспользоваться тригонометрическими формулами
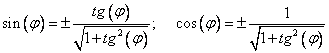
Знак выбирается в зависимости от того, в какой четверти лежит угол, а, так как без разницы на какой угол поворачивать систему координат, лишь бы смешанное произведение 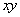ушло, то выберем «+».
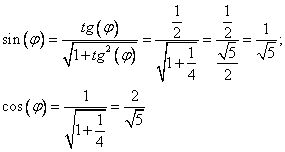
Замена:
Вывод: Слагаемых 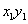нет.
ШАГ ВТОРОЙ
На данный момент имеется: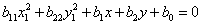 
(смешанных произведений координат нет.)
Пример:
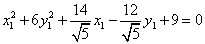
Теперь, для каждой переменной, для которой коэффициенты при квадрате и при первой степени ненулевые следует применить выделение полного квадрата:
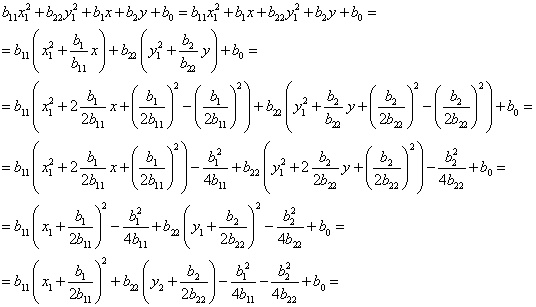
И сделать соответствующую замену:
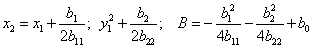
Уравнение примет вид:
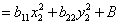
Пример:
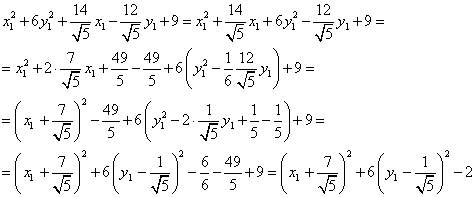
Замена:
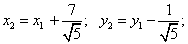
Вывод: Уравнение примет вид:
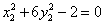
ШАГ ТРЕТИЙ, ОКОНЧАТЕЛЬНЫЙ.
Итак, имеется уравнение
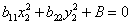
Пример:
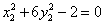
Остались последние алгебраические преобразования:
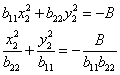
После чего можно определять тип кривой второго порядка по таблице, приведенной на предыдущей странице.
Пример:
Это эллипс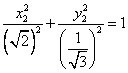 
, полуоси 
.
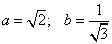Вывод:
Для того, чтобы привести кривую второго порядка 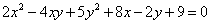к каноническому виду и определить тип кривой было сделано две замены:
1) 
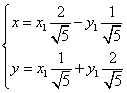
, которая повернула систему координат на угол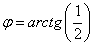 
2) 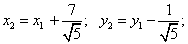— сдвинувшая начало координат.
Объединим замены:
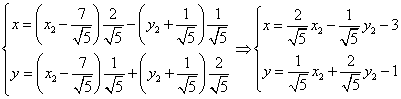
Заметим, что начало координат окончательной системы координат расположено в точке с координатами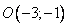 
.
