В этой статье будут показаны примеры некоторых алгоритмов для работы с B-сплайнами, в основном по мотивам книги “The NURBS Book”. Здесь не будут рассматриваться тонкие моменты и разнообразные случаи, а лишь более-менее общий вариант задания и построения сплайнов.
Основные определения
Замечание: термины могут не совпадать с аналогичными в различных книгах как на русском, так и на английском языках.
Пусть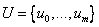 
— неубывающая последовательность рациональных чисел.
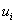будем называть узлами, а 
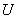— узловым вектором.
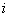-ую базисную функцию В-сплайна степени p (порядок 
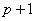) будем обозначать 
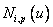и определим как
Невооруженным глазом видно, что базисные функции определяются рекуррентно. Для вычисления соответствующей базисной функции удобно осознать и использовать следующую треугольную таблицу
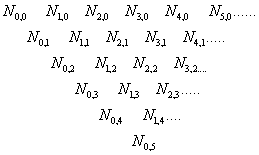
Т.е. например, для того, чтобы определить
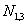, необходимо найти значения базисных функций 
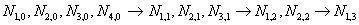. Все это долго, но мы справимся.
В-сплайном степени p называется кривая, определяемая как
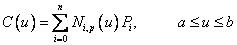
, где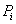 
— контрольные точки, 
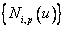— базисные функции степени p, определенные на непериодическом и неоднородном векторе узловых точек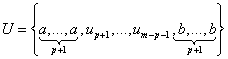 
1. Построение кривой
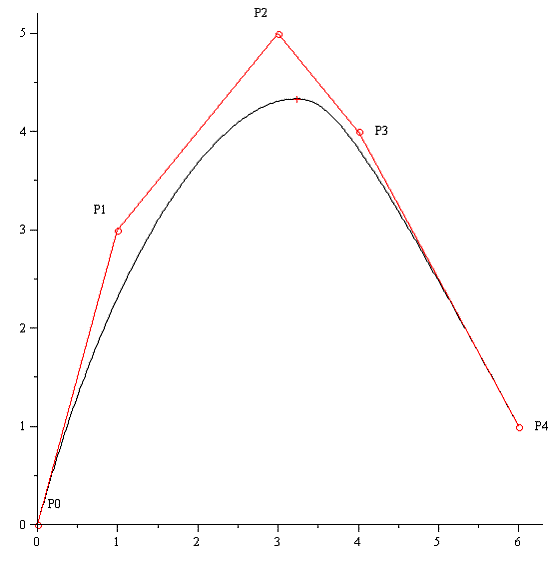
Построим кривую В-сплайнами третьей степени по контрольным точкам
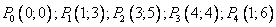.Точек 5, степень 3-я, т.е. узлов должно быть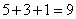 
.
Пусть вектор узловых точек имеет вид: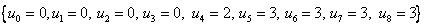 
,
т.е. параметр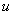 
изменяет свои значения от 0 до 3.
Важные замечания: Чаще всего используются так называемые непериодические узловые векторы, т.е. типа 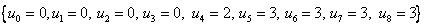, здесь первые и последние компоненты равны друг другу по 4 шт, отсюда можно сделать вывод, что степень базисных функций будет 
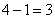, а, соответственно, контрольных точек обрабатывается 
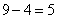(9 узлов – 4 одинаковых значения). Конечно же, существуют и периодические узловые векторы и т.д., но о них позже и их методы обработки не отличаются совершенно от рассмотренных ниже.
Распишем функцию:
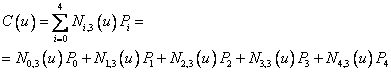
Определим базисные функции для В-сплайнов в соответствии с таблицей:
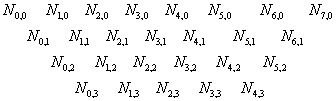
Первая строка
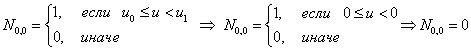
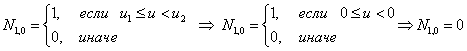
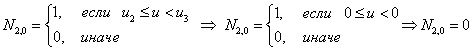
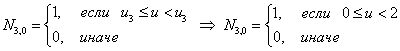
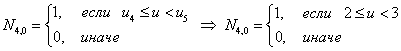
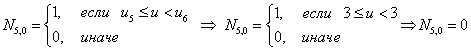
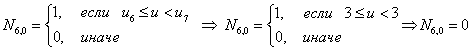
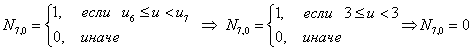
Итого, первая строка из треугольной таблицы необходимых базисных функций В-сплайна:
Вторая строка
По треугольной таблице для базисной функции, т.к.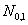 
является комбинацией 
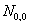и 
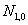, а они оба равны нулю, то и 
.
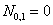Аналогично с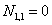 
, 
.
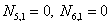Сложнее с другими:
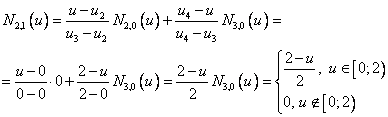
Следующий
И еще один
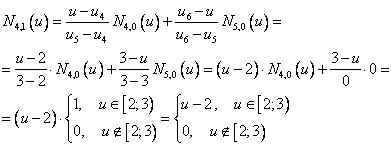
Остальные уже обсудили, они равны нулю.
Итого, по второй строке:
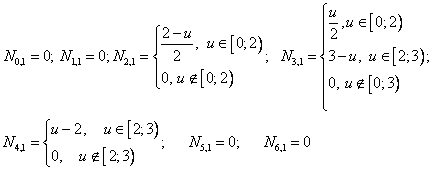
Третья строка
По треугольной таблице для базисной функции, т.к.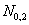 
является комбинацие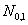й и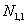 
, а они оба равны нулю, то и 
.
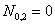Аналогично с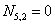 
.
Вычислим остальные из третьей строки:
Следующий
И еще один
И последний в этой строке:
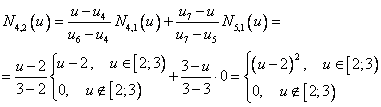
Итого, по строке
Четвертая строка (последняя)
Далее
Итого, искомые базисные функции для B-сплайнов имеют вид:
Вспомним искомое:
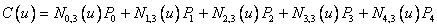
Составим параметрическое уравнение кривой:
1) При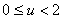 
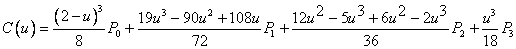
2) При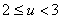 
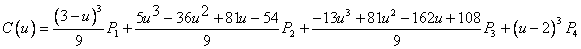
Подставим координаты точек:
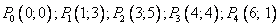
1) При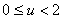
2) При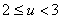
Итого
1) При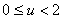
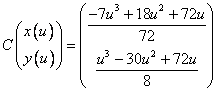
2) При
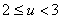
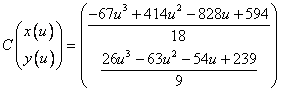
Построим ограничивающий (контрольный) многоугольник (соединив контрольные точки) и искомую кривую. Разным цветом указаны сплайны пр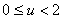и
и 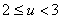.