Один из важных разделов элементарной математики – текстовые задачи на составление уравнений и неравенств. Один из типов таких задач – задачи на смеси, растворы, процентное и долевое содержание. Рассматриваемый в этой статье метод решения этого типа задач обладает некоторой избыточностью (то есть производятся лишние вычислиения), однако является практически универсальным.

Чаще всего объектом математического исследования подобных задач является смесь каких-либо двух или более веществ. Каждую такую смесь удобно представлять в виде таблицы:

Масса (объем)  всей смеси
Доля  вещества №1	Доля  вещества №2
Масса (объем)  вещества №1	Масса (объем)  вещества №2

 

Пример 1.

Описать с помощью таблицы 10 тонн молока жирностью 3,5 %.

Решение:

Т.к. в таблицу заносится доля, то доля жира: 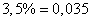. Доля воды, соответственно: .

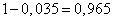Будем считать, что молоко представляет собой смесь жира и воды.

Масса всей смеси  10 тонн
Доля жира  0,035	Доля воды  0,965
Масса жират	Масса воды  т

 

Замечание: При заполнении полей таблицы использовалась одна из основных формул для этого типа задач:

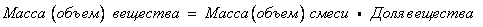
Из этого равенства можно выражать любую его часть:

Пример 2.

Описать с помощью таблицы смесь азотной и соляной кислот, если известно, что доля азотной кислоты 0,4, а её масса 430 кг.

Решение:

Определим массу всей смеси по формуле:

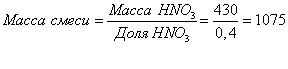
Остальные ячейки таблицы тоже необходимо заполнить:

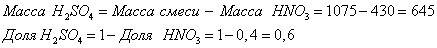
Масса всей смеси  1075 кг
Доля  0,4	Доля  0,6
Масса  430 кг	Масса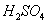  645 кг

 

Примеры решения простейших задач.

Пример 3.

Для хранения было положено 1000 кг грибов, имеющих влажность 99%. После некоторой усушки влажность грибов составила 98%. Определить Г – вес грибов после усушки.

Решение:

Будем считать (и это на самом деле так), что грибы состоят из воды и сухого вещества.

Опишем грибы до усушки с помощью таблицы.

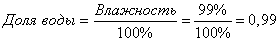
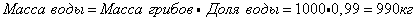
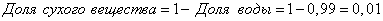
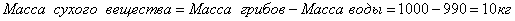
Масса грибов  1000 кг
Доля воды 0,99	Доля сух. в-ва 0,01
Масса воды 990кг	Масса сух. в-ва 10кг

Замечание: Следует понимать, что всегда сумма второй строки таблицы должна быть равна 1, а сумма третьей строки должна быть равна массе всей смеси.

В условии задачи сказано, что грибы проходят усушку, то есть из грибов испаряется вода. Обозначим массу испарившейся воды как  кг. Запишем эту воду в виде таблицы.

Масса испарившейся воды х кг
Доля воды 1	Доля сух. в-ва 0
Масса воды х кг	Масса сух. в-ва 0 кг

Заполнение таблицы становится очевидным после осознавания того факта, что доля воды в воде это 1, а сухого вещества в воде попросту нет.

Процесс усушки – это разность:

Масса грибов 1000 кг			Масса испарившейся воды х кг
Доля воды 0,99	Доля сух. в-ва 0,01	—	Доля воды 1	Доля сух. в-ва 0
Масса воды 990кг	Масса сух. в-ва 10кг		Масса воды х кг	Масса сух. в-ва 0 кг

Составим таблицу, описывающую результат этого вычитания. Итогом усушки ( т.е. вычитания воды из грибов) будут сухие грибы.

Замечание: Вычитать и складывать можно только килограммы, доли вычитать, складывать или делить нельзя.

1000 кг			x кг			1000-x кг
0,99	0,01	___	1	0	=
990кг	10кг		x кг	0 кг		990-x кг	10 кг

 

Возникает резонный вопрос: как же заполнить вторую строку результирующей таблицы? Как же узнать доли полученной смеси? И еще раз обратим внимание на формулу:

Про сухое вещество аналогично.

Итак, грибы после усушки описаны в таблице:

1000 кг			x кг			1000-x кг
0,99	0,01	___	1	0	=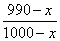
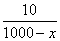990кг	10кг		x кг	0 кг		990-x кг	10 кг

 

Составление уравнения:

Еще раз прочтя условие можно обнаружить, что после усушки влажность грибов составила 98%. То есть доля воды в грибах стала 0,98. А где в таблице-результате доля грибов? Во второй строке, первом столбце.

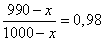
Решение этого уравнение не представляет труда.

Выпарилось 500 кг.  В задаче спрашивается: определить Г – вес грибов после усушки.

Г=1000-500=500

Ответ: Г=500 кг (вес грибов после усушки).

Замечание: Решение растянуто исключительно ради подробного объяснения.

 

Пример 4.

Имеется две смеси апельсинового и ананасного соков. Смесь-1 содержит 40% апельсинового сока; смесь-2 содержит 80% апельсинового сока. Сливается p литров смеси-1 и q литров смеси-2, и получается 20 литров смеси, содержащей 70% апельсинового сока.  Определить p и q.

Решение:

Таблицы составляются в виде:

Объем смеси
Доля апельсинового сока	Доля ананасного сока
Объем апельсинового сока	Объем ананасного сока

 

 

Смесь-1:

Объем смеси = p

Доля ананасного сока = 0,4

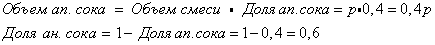
p л
0,4	0,6
0,4p л	0,6p л

 

Смесь-2:

 

q л
0,8	0,2
0,8q л	0,2q л

 

Их смешивают. Помним, что нельзя складывать доли, складывать можно только литры.

p л			q л			p+q л
0,4	0,6	+	0,8	0,2	=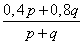
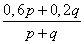0,4p л	0,6p л		0,8q л	0,2q л		0,4p +0,8q л	0,6p + 0,2q л

 

Возвращаемся к тексту задачи и действуем по методы «один факт – одно уравнение».

1)      «и получается 20 литров смеси» :

 
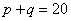
2)      «содержащей 70% апельсинового сока»

 
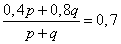
Получилась система из двух уравнений и двух неизвестных.

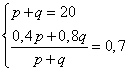
Из первого уравнения следует выразить p и подставить во второе.

 

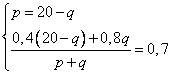
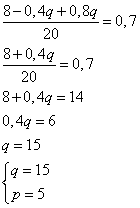
Ответ: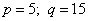

Пример 5.

Имеется две смеси сухофруктов. В смеси-1 отношение веса яблок к весу груш равно 2; в смеси-2 это отношение равно 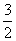. Определить x и y – количества смеси-1 и смеси-2 соответственно, которые надо взять для получения 38 кг смеси, в которой отношение веса яблок к весу груш равно .

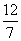Решение:

В условии этой задачи не указаны в привычной форме записи концентрации яблок и груш, или их доли, или их процентное содержание в смесях.

В смеси-1 отношение веса яблок к весу груш равно 2.

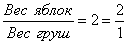
То есть вес яблок это две доли, вес груш это одна доля. Всего долей получается 3. Таким образом, вес яблок составляет 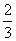 от веса смеси-1, а вес груш —  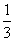 от веса смеси-1.

x кг
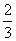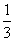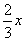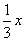кг	кг

В смеси-2 отношение веса яблок к весу груш равно .

 

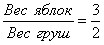
То есть вес яблок это три доли, вес груш это две доли. Всего долей получается 5. Вес яблок составляет 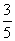 от веса смеси-2, а вес груш —  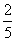 от веса смеси-2.

 

y кг
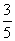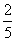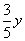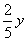кг	кг

 

Смешиваем.

x кг			y кг			x+y кг
		+			=
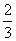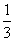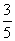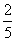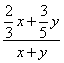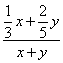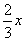кг	кг		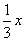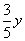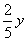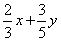кг	кг		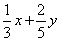кг	кг

 

Составляем уравнения:

1)      «которые надо взять для получения 38 кг смеси»

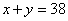
2)      «в которой отношение веса яблок к весу груш равно »

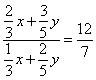
Получилась система из двух уравнений и двух неизвестных. Решим ее.

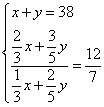
Выразим из первого уравнения x и подставим во второе.

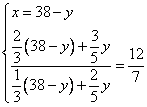
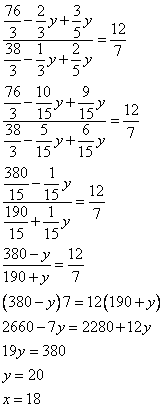
Ответ: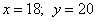

 

 

Условие задач любезно предоставлены :

1. Тынянкин С.А., Тырымов А.А. «Повторении и контроль  знаний. Математика. Книга 5. Сборник практических задач. 9-11 классы. Подготовка к ГИА и ЕГЭ. 4300 конкурсных задач (ответы, указания, решения)»

 

Понравилась статья?