Элементы числовой последовательности действительных чисел удобно изображать на числовой прямой, при этом они могут быть расположены на ней хаотично (не подчинено никакому закону или правилу) или как то упорядоченно.
Они могут стремиться к какому-то числу. Т.е. с возрастанием номера элемент становится все ближе и ближе к какому -то числу.

Определение:
Число А называется пределом числовой последовательности 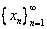если для любого числа 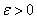существует такой номер 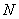, зависящий от 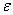, что, начиная с этого номера все элементы последовательности удалены от А не более чем на 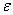(принадлежат 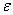-окрестности числа А). И обозначается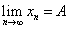
Замечание:
В математике общепринятыми считаются обозначения:
1)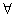 , заменяет словосочетание «для любого».
2) 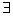, заменяет слово «существует».

Определение (на языке «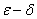 » (читается «на языке эпсилон-дельта»)):
Число А называется пределом числовой последовательности 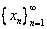если :

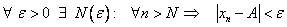
Обозначается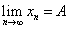
Пример:
Доказать, что пределом последовательности 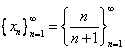при стремлении к бесконечности является 1.

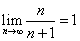
Доказательство:
Доказать, что число является пределом последовательности означает указать закон, по которому, выбрав произвольное 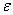, можно найти номер, начиная с которого элементы последовательности будут лежать в 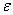-окрестности этого числа.
1. Итак, требуется выполнение неравенства

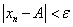
Подставим выражение для общего члена последовательности и значение предела из условия этой задачи

Т.к. 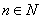(т.е. положительное), то можно раскрыть модуль

Выразим из полученного неравенства:

2.
Приравняем .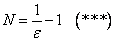
Полученное выражение и есть искомый закон, по которому, выбрав произвольное 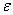, можно найти номер, начиная с которого элементы последовательности будут лежать в 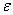-окрестности этого числа.
Давайте разберемся.
а) выбираем произвольное .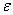
б) подставляем его в выражение (***) и находим значение .
в) для любого 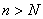будет верно неравенство (**) потому, что правая часть неравенства (**) и есть значение, которое присвоено .
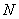г) а неравенство (**) равносильно неравенству (*) (это оно же, только преобразованное), т.е. для любого числа 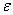можно указать такой номер 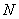, что, начиная с этого номера, все элементы последовательности удалены от 1 не более чем на 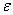, а значит 1 является пределом последовательности.
Пример:
Известно, что 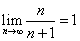. Требуется найти 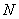для:
а)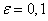
б)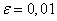
в)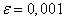
Решение:
В предыдущем примере была найдена функциональная зависимость между 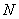и :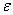
.
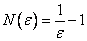а) 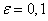, , 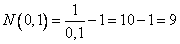т.е. , начиная с 10-го номера все элементы последовательности отстоят от 1 не более, чем на 0,1.
Вычислим несколько значений элементов:

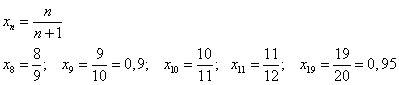
Отметим их на числовой оси.

б) ,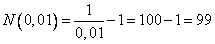
т.е. , начиная с 100-го номера все элементы последовательности отстоят от 1 не более, чем на 0,01.
Рис.
в) ,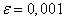
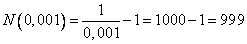
т.е. , начиная с 1000-го номера все элементы последовательности отстоят от 1 не более, чем на 0,001.