Оглавление.

1. Числовая последовательность.
2. Предел числовой последовательности.
3. Примеры вычисления пределов числовых последовательностей.
4. Предел функции.
5. Основные методы вычисления пределов.

В этой статья будут описаны некоторые приемы и методы для того, чтобы найти (вычислить) пределы числовых последовательностей и функций.

Теоретическая часть.

Определение («простым языком»): Числовой последовательностью называется занумерованный набор чисел.
Определение: Числовой последовательностью называется такое множество чисел (действительных или комплексных), для которого задано взаимно однозначное соответствие со множеством натуральных чисел.
Пример и обозначения:
Множество чисел: 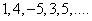можно рассматривать как числовую последовательность, если пронумеровать элементы этого множества, например:

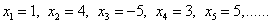
Все множество обозначается: .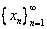
Замечание: В рассмотренном выше примере множество – просто набор цифр «с потолка». В математическом анализе, как правило, работают с такими последовательностями, в которых можно задать общий член последовательности, т.е. закон, по которому, зная номер элемента, можно вычислить сам элемент.
Пример:
Пусть известны первые несколько членов последовательности:

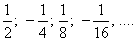
Выяснить вид общего члена этой последовательности.
Решение:
Проведем анализ имеющихся элементов:
а) элементы представляют собой дробь, т.е. общий вид будет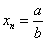
б) в числителе всех элементов стоит 1, т.е. общий вид будет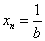
в) знаки чередуются начиная с «+», т.е. общий вид будет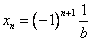
г) в знаменателях стоят степени двойки, начиная с первой, т.е. общий вид будет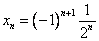
Проверка: Вычислим третий элемент последовательности: .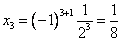
Итог: Общий вид элементов последовательности : 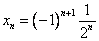, где .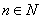
Пример: Числовая последовательность задана формулой n-го члена:

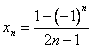
Выписать первые пять элементов последовательности.
Решение:
1)

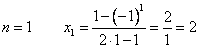
2)
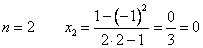
3)
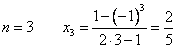
4)
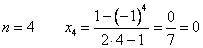
5)
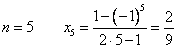
Итог:
Проанализируем полученную последовательность.
а) Элементы, стоящие на четных местах равны нулю.
б) Элементы, стоящие на нечетных местах представляют из себя дроби, в числителе которых стоят 2, а в знаменателе – нечетные числа «через одного».