Определение:
Говорят, что функция  имеет пределом число
имеет пределом число  , при стремлении
, при стремлении  к
к 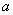 (или в точке
(или в точке 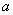 ), если для каждого числа
), если для каждого числа 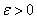 найдется такое число
найдется такое число 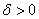 , что, как только неравенство
, что, как только неравенство

становится верным, то верным становится и неравенство
 .
.
Обозначают этот факт так:

Замечание: это определение называют определением «по Коши». Существует также равносильное ему определение предела последовательность «по Гейне», в котором определение дается через последовательности.
Изобразим графически определение предела функции:
1) Есть функция  ,
, 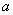 ,
,  :
:

2) Выберем произвольное положительное эпсилон (построим эпсилон- окрестность точки  )
)
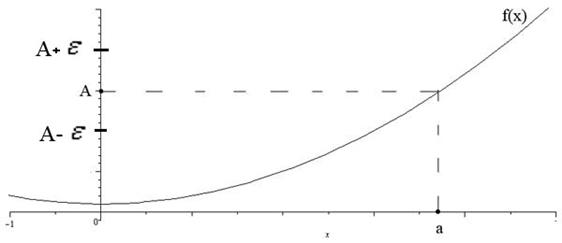
3) К выбранному эпсилон подберем значение дельты и построим дельта-окрестность точки 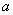
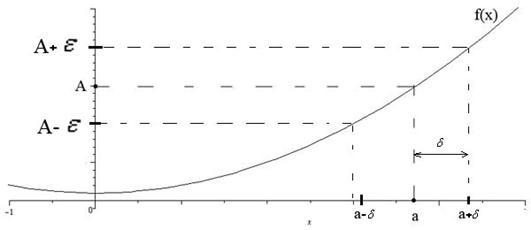
4) Как только  будет попадать в
будет попадать в  -окрестность точки
-окрестность точки 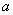 , то будет попадать в
, то будет попадать в 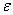 -окрестность точки
-окрестность точки  , т.е. из неравенства
, т.е. из неравенства  следует неравенство
следует неравенство  .
.

Замечание:
Серой полосой отмечена отображение всей  -окрестности на ось ординат для того, чтобы показать, что вся она лежит в
-окрестности на ось ординат для того, чтобы показать, что вся она лежит в 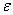 -окрестности точки А.
-окрестности точки А.
Картинку рекомендуется осознать и запомнить, т.к. на экзамене она очень помогает составить длинное и непонятное определение предела языком эпсилон-дельта.


