Сейчас будет разобран несколько другой метод решения этой же задачи с использованием термина «скорость сближения».
Замечание: Если два предмета двигаются на встречу друг другу, то их скорость сближения равна сумме их скоростей. Если же один догоняет другого, то их скорость сближения равна разности скорость догоняющего и догоняемого. Если она положительна, то встреча произойдет, а если она отрицательна, то скорость догоняющего меньше скорости догоняемого и они никогда не встретятся. Печально.
Задача:
Из пункта А выехал грузовой автомобиль со скоростью 40 км/ч. Через час по той же дороге и в том же направлении выехал еще один грузовой автомобиль, но со скоростью 50 км/ч. Еще через час по той же дороге и в том же направлении выехал легковой автомобиль. Легковой автомобиль догонит первый грузовик через 21 минуту после того, как он догонит второй грузовик.
Чему равна скорость движения легкового автомобиля?
Решение:
План: за переменную будем обозначать скорость, а уравнение составлять по времени, т.к. известно, что время до встречи второго и третьего отличается от времени до встречи первого и третьего на 21 минуту.
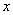 км/ч – скорость движения легкового автомобиля.
км/ч – скорость движения легкового автомобиля.
Ситуация, описанная в задаче предельно ясна. Выехал один, прошел час – выехал второй, прошел еще час – выехал третий.
Разберем две ситуации:
1) Третий догнал второго.
На момент начала движения третьим второй двигался уже час со скоростью 50 км/ч, т.е. прошел 50 км.
Между догоняющим и догоняемым 50 км.
Они двигаются в одном направлении, значит их скорость сближения равна 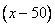 км/ч.
км/ч.
Время, за которое можно пройти 50 км с этой скоростью: 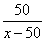 часов.
часов.
Это и есть время, за которое третий догонит второго.
2) Третий догнал первого.
На момент начала движения третьим первый двигался уже 2 часа со скоростью 40 км/ч, т.е. прошел 80 км.
Между догоняющим и догоняемым 80 км.
Они двигаются в одном направлении, значит их скорость сближения равна 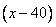 км/ч.
км/ч.
Время, за которое можно пройти 80 км с этой скоростью: 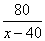 часов.
часов.
Это и есть время, за которое третий догонит первого.
Составление уравнения:
Из условия известно, что третий догонит первого спустя 21 минуту после встречи со вторым. Переведем в часы: 21 минута = 0,35 часа.

Ответ: Скорость легкового автомобиля 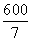 или 90 км/ч.
или 90 км/ч.
Результаты сходятся с первым методом.
Вывод: Оба предложенных метода долее или менее удобны для разных задач на движение. Первый обладает наглядностью, но несколько громоздок, второй – краткостью записи, но требует абсолютного понимания «ситуации на дороге». Но оба они дают результат, причем верный. Дальше выбирать вам.


