Вспомним производственную задачу линейного программирования, решенную в предыдущем параграфе симплекс-методом.
Задача:

Предприятие выпускает 4 вида изделий, имея 3 группы оборудования. Нормы времени на обработку каждого изделия на каждой группе оборудования заданы матрицей А, фонд времени работы каждой группы оборудования задан матрицей В. Требуется составить такой план производства, при котором прибыль предприятия будет наибольшей.

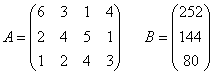
Прибыль на единицу изделия соответствующей группы задана матрицей:

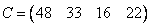
Результаты, полученные в предыдущем параграфе
Вывод: для максимальной выручки в размере 2196 следует выпускать продукцию первого типа в объеме 32 шт, второго типа – 20 шт., при этот остатки ресурсов третьего типа составят 8 единиц.

В оптимальной производственной программе

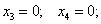
Предположим, что продукцию третьего и четвертого типа производить намерения не было. Рассмотрим задачу с оставшимися переменными, сохранив их нумерацию, и, решив эту задачу графически, убедимся в правильности решения симплексным методом.

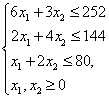
1)Построим граничные прямые и выберем соответствующие полуплоскости, приняв переменную 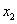за ординату, а
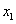— за абсциссу.

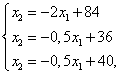— граничные прямые

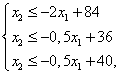— полуплоскости.

2) Целевая функция :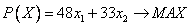

Построим вектор градиент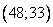

3) Проведем и сдвинем линию, перпендикулярную вектор градиенты, в направлении вектор-градиента до тех пор, пока она не станет опорной к области допустимых решений.

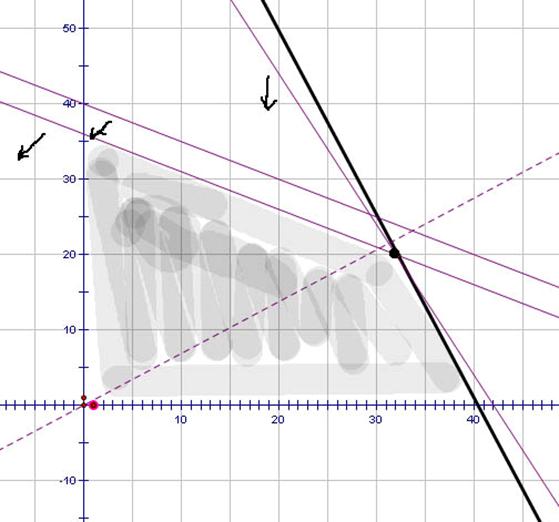
Точка пересечения прямой и области допустимых значений — точка пересечения прямых

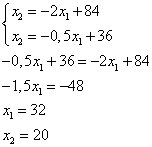
Вывод: Это доказывает, что задача решена симплекс методом верно.