Матрицы – объект-новинка для человека, поступившего в высшее учебное заведение. В школе учителя оперируют лишь такими объектами как число и вектор. А тут вон оно чего. Оказывается все это матрицы.
Определение: матрицей называется множество чисел, записанных в виде таблицы, причем каждому элементу этого множества (элементу матрицы) ставится в соответствие пара чисел, первое из которых обозначает номер строки, а второе — номер столбца, в которых расположен этот элемент.
Пример:

Да, все это матрицы, просто число это, с определенным допуском, матрица размера 1 на 1, вектор трехмерного пространства, например  — матрица размера 1 на 3. И т.д. Мы живем в мире матриц.
— матрица размера 1 на 3. И т.д. Мы живем в мире матриц.
Конечно же, к этим элементам можно применять основные математические операции – сложение, умножение и умножение матрицы на число. Определим эти операции.
Сложение матриц.
Складывать можно только матрицы одного размера. При сложении двух матрицы складываются соответствующие их элементы, т.е.
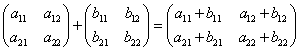
Пример:
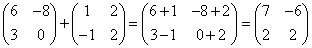
2) Умножение матрицы на число.
При умножении матрицы на число все элементы матрицы умножаются на этой число.
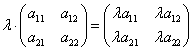
Пример:
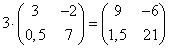
3) Умножение матриц.
Тут нужно запомнить два факта:
А) Произведение матрица 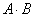 определено, если количество столбцов первой матрицы равно количеству строк второй матрицы.
определено, если количество столбцов первой матрицы равно количеству строк второй матрицы.
Б) Вообще говоря, операция умножения матриц не обладает свойством коммутативности ( ), т.е.
), т.е. 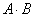 может быть равно
может быть равно  только в исключительных случаях.
только в исключительных случаях.
Матрицы, для которых верно равенство  называются перестановочными.
называются перестановочными.
Еще надо запомнить одну фразу, в которой и сокрыт принцип умножения матриц:
«Строка на столбец».
Покажем умножение на примере двух матриц размера 2х2

А теперь общий принцип: если требуется перемножить две матрицы, то для того, чтобы вычислить элемент с номером  требуется из первой матрицы взять строку с номером
требуется из первой матрицы взять строку с номером  , из второй матрицы – столбец с номером
, из второй матрицы – столбец с номером  , и записать сумму произведений соответствующих координат.
, и записать сумму произведений соответствующих координат.

Для матриц еще определены операции вычисления обратной матрицы и вычисления определителя, но о них рассказано в других статьях этого раздела.
Вычисление определителей.
О том, как найти обратную матрицу.


