Как найти обратную матрицу?

В этой статье рассматриваются два метода нахождения матрицы, обратной к данной.
Определение:
Матрицей, обратной к матрице А называется такая матрица, которая при умножении на исходную дает единичную матрицу. Порядок умножения матриц неважен. Обозначается обратная матрица .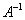

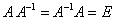
Метод 1. С помощью матрицы алгебраических дополнений (наиболее часто применяемый).

Задача:
Дана матрица . Требуется вычислить обратную к ней матрицу .
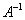Алгоритм решения:
1) Вычислить определитель матрицы .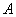

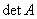
2) Составить матрицу алгебраических дополнений к элементам матрицы .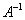

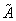
3) Транспонировать матрицу алгебраических дополнений.

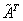
4) Каждый элемент матрицы разделить на 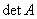. Полученная матрица и будет обратной к исходной.

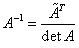
5) Проверка.
.

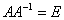Пример:
Задача:
Дана матрица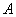
.
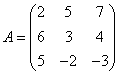Требуется вычислить обратную к ней матрицу .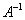
Решение:
1) Найдем определитель этой матрицы.

2) Составим матрицу алгебраических дополнений к элементам матрицы .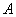
Найдем алгебраическое дополнение к элементу 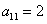. Для этого нужно вычислить минор, получаемый вычеркиванием первой строки и первого столбца, и умножить этот минор на минус единицу в степени суммы индексов.


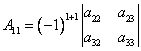
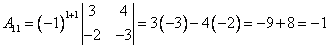
Аналогично найдем алгебраические дополнения к остальным элементам матрицы.

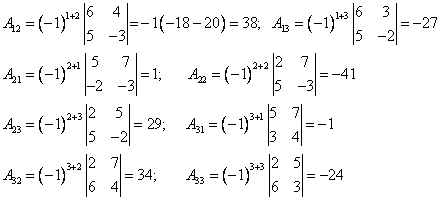
Составим матрицу алгебраических дополнений

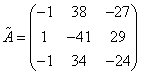
3) Транспонируем матрицу алгебраических дополнений.

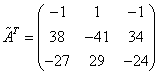
4) Каждый элемент матрицы разделим на 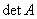. Полученная матрица и будет обратной к исходной.

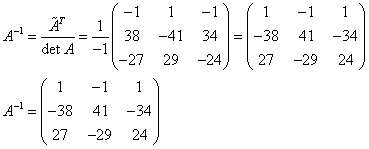
5) Проверка.

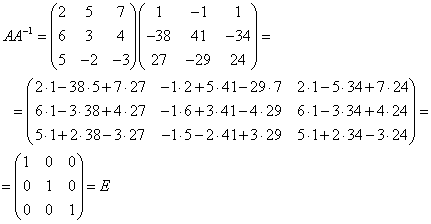
Ответ: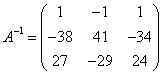

Метод 2. С помощью присоединенной матрицы (практически не применяемый метод).

Задача:
Дана матрица 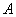. Требуется вычислить обратную к ней матрицу .
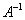Алгоритм решения:
1) Записать исходную матрицу с присоединенной к ней единичной.

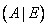
2) Алгебраическими преобразованиями, проводимыми со строками полученной составной матрицы приводим ее к такому виду, чтобы в левой половине стояла единичная матрица. Тогда в правой половине будет стоять матрица .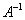

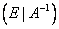
3) Проверка.
.

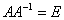Пример:

Задача:
Дана матрица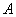
.
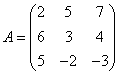Требуется вычислить обратную к ней матрицу .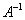
Решение:
1) Записать исходную матрицу с присоединенной к ней единичной.

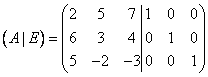
2) Алгебраическими преобразованиями, проводимыми со строками полученной составной матрицы приводим ее к такому виду, чтобы в левой половине стояла единичная матрица. Тогда в правой половине будет стоять матрица .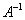

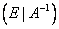
Разрешено:
а) к элементам строки прибавлять элементы другой строки, умноженные на одно и то же число;
б) все элементы строки умножать на одно и то же число (отличное от нуля).

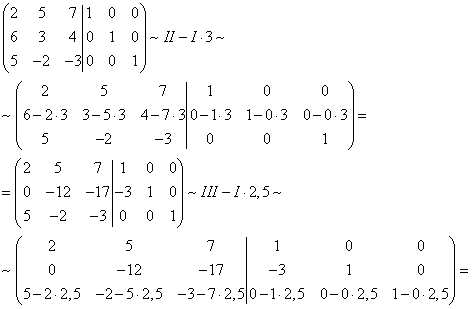
Продолжаем….

Не отвлекаемся….

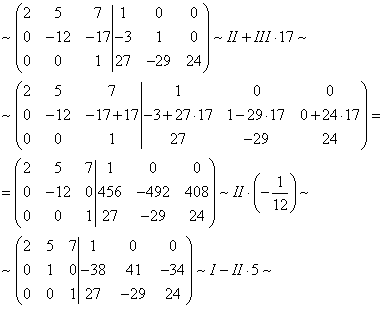
Осталось совсем чуть-чуть….

3) Проверка (проводилась в предыдущем примере).
.
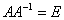Ответ: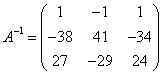
Замечание: По объему выкладок становится ясно, что если матрица не какой- либо специальной формы, то быстрее пользоваться первым рассмотренным методом.