Оглавление.
1. Определители. Вычисление определителей 1-го, 2-го и 3-го порядков.
2. Определители n-го порядка.
3. Теорема Лапласа.
4.Применение теоремы Лапласа для вычисления определителей n-го порядка (разложение по строке или столбцу).
4.Свойства определителей.
5.Пример вычисления определителя с помощью свойств.
6.Пример вычисления определителя методом выделения линейных множителей.
7.Пример вычисления определителей методом рекурентных соотношений.
Определители.
Теоретическая часть.
Предполагается, что читателю уже известен такой математический объект как матрица.
Определение:
Матрицей называется множество чисел, записанное в виде таблицы, где каждому числу ( элементу матрицы) соответствует двойной индекс, первая часть которого означает номер строки, в которой расположено это число, а вторая – номер столбца. Эта таблица чисел заключается в круглые скобки.
Матрица называется квадратной, если количество её строк равно количеству столбцов.
Пример:
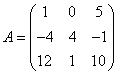
— матрица А размера 3 на 3, её элемент, например,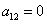 
( 1-я строка, 2-ой столбец).
Итак, теперь об определителях.
Замечание: Иногда определители называют на английский манер детерминантами, это одно и то же (для тех, кто знает английский язык и подавно).
Определение 1 (простое, для нематематических людей и специальностей):
Определителем матрицы называется некоторая математическая функция элементов квадратной матрицы, результатом которой является число.
Обозначение:
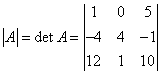— определитель 3- го порядка (т.к. матрица размера 3 на 3) матрицы А.
Замечание: В этом, якобы простом, определении определителя ( звучит как тавтология) говориться, что с элементами матрицы нужно что то сделать ( умножить, сложить, разделить и т.д.) и получится значение определителя этой матрицы. Однако не сказано. Что же все-таки надо с ними сделать.
Вычисление определителей первого порядка.
Матрица размера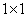 
это просто число. Определителем такой матрицы является само это число.
Пример:
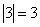
Вычисление определителей второго порядка.
Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:
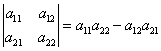
Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.
Пример:
.
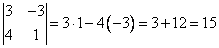Вычисление определителей третьего порядка.
Определитель третьего порядка вычисляется по правилу:
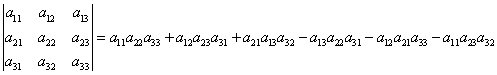
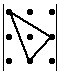
Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников:
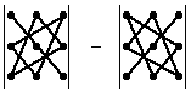
Здесь схематично показано, какие сомножители соседствуют в слагаемых.
Пример:
Вычислить определитель:
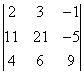
Решение:
Воспользуемся правилом треугольников.
Объясним картинку подробно, т.е. распишем каждое слагаемое отдельно:
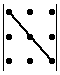
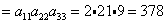
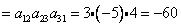
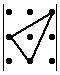
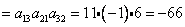
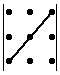
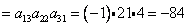
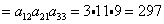
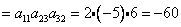
Итого:
Ответ: 108