Перечислим все свойства определителей без доказательства, т.к. целью этого цикла статей является практическое применение знаний и вычисление определителей в частности.
1. Определитель не меняется при транспонировании.
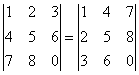
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
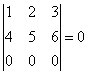
3. От перестановки двух строк определитель меняет знак.
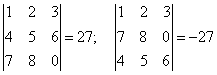
4. Определитель, содержащий две одинаковые строки равен нулю.
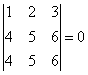
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
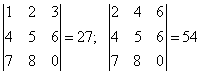
6. Определитель, содержащий две пропорциональные строки, равен нулю.
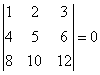
7. Если все элементы i-ой строки определителя n-го порядка представлены в виде суммы двух слагаемых:
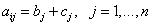 ,
,
то определитель равен сумме двух определителей, у которых все строки кроме i-ой. – такие же, как и в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов 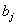 , а в другом — из элементов
, а в другом — из элементов 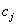 .
.
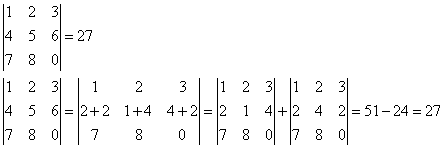
8. Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю.
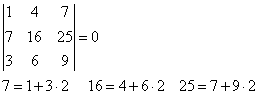
9. Определитель не меняется, если к элементам одной из его строк прибавляются соответственные элементы другой строки, умноженные на одно и то же число.

Замечание: Обратим внимание на последний определитель. Следует запомнить, что если определитель приведен к верхнетреугольному виду, т.е. если все элементы определителя, стоящие под главной диагональю, равны нулю, то определитель равен произведению элементов, стоящих на главной диагонали.


