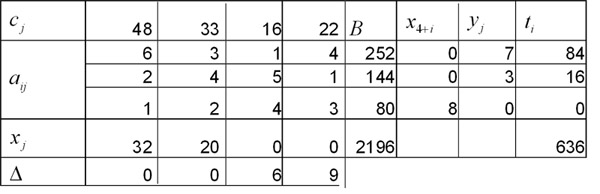
Продолжаем решение задачи, начатое в предыдущих параграфах.

При выполнении оптимальной производственной программы первый и второй ресурсы используются полностью, т.е. образуют «узкие места производства». Их следует заказать дополнительно.

Обозначим 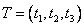— вектор дополнительных объемов ресурсов. Причем уже известно, что .

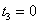Т.к. будут использоваться найденные в предыдущей задаче двойственные оценки ресурсов, то должно быть выполнено условие:
,
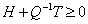Где 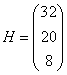, 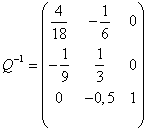— эти матрицы взяты из последней симплекс таблицы.

Запишем и преобразуем матричное неравенство:

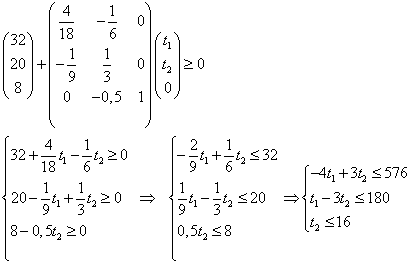
Задача состоит в том, чтобы найти вектор 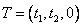максимизирующий суммарный прирост прибыли

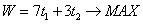
при условии сохранения двойственных оценок ресурсов, предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида.

Запишем матричное неравенство

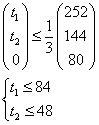
Итого, получена задача линейного программирования:

Требуется максимизировать 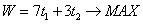при условиях

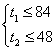
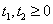
Решим эту задачу графически.

1)Построим граничные прямые и выберем соответствующие полуплоскости, приняв переменную ординату, а — за абсциссу.
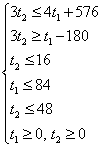— полуплоскости
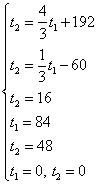— граничные прямые.
2) Целевая функция :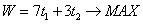
Построим вектор градиент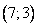
3) Проведем и сдвинем линию, перпендикулярную вектор градиенты, в направлении вектор-градиента до тех пор, пока она не станет опорной к области допустимых решений.

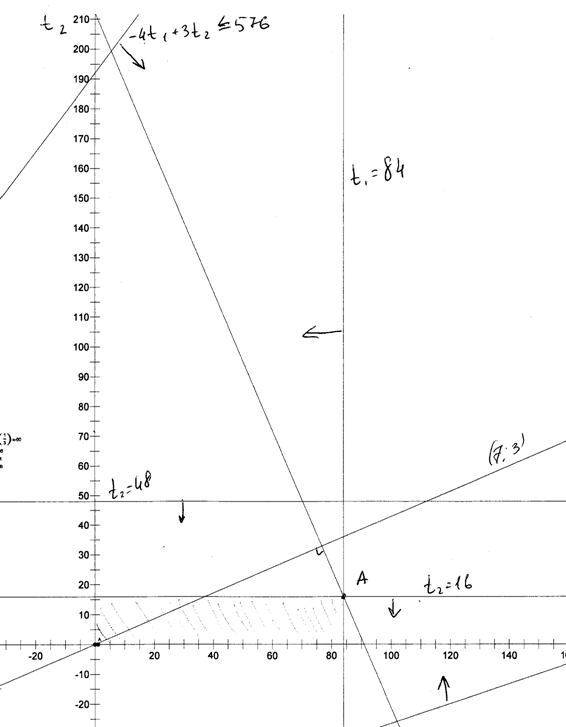
Координаты точки А: , т.о.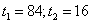
И программа «расшивки», т.е. размер дополнительных ресурсов, имеет вид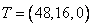

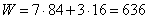— прирост прибыли.

Проведем сводку результатов исследования производственной задачи: