Назад Оглавление

Найти решение системы 4 линейных уравнений с 4-мя неизвестными 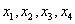с точностью до 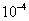методом простой итерации;

Решение:
Исходная система:

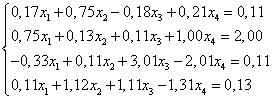
Рассмотрим преобразованную систему из предыдущего случая

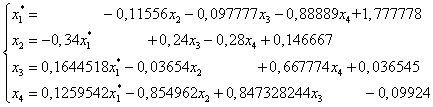
Метод Зейделя заключается в итерационном процесс, который можно записать в виде:

Выберем начальное приближение – столбец свободных членов, т.е.


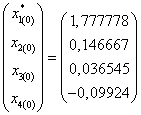
Занесем результаты вычислений в таблицу

1	2	3	4	5	6	7	8
1,845467	1,801529	1,715977	1,673689	1,650408	1,638189	1,631668	1,628208
-0,44423	-0,39601	-0,37676	-0,36386	-0,35749	-0,35401	-0,35218	-0,3512
0,290002	0,346701	0,387848	0,407497	0,418362	0,424054	0,427093	0,428705
-0,00087	0,08287	0,123416	0,145769	0,157491	0,163749	0,167069	0,168834

 

9	10	11	12	13	14	15
1,626369	1,625391	1,624872	1,624596	1,62445	1,624372	1,624331
-0,35068	-0,35041	-0,35026	-0,35018	-0,35014	-0,35012	-0,35011
0,429563	0,430018	0,43026	0,430389	0,430457	0,430493	0,430512
0,169771	0,17027	0,170534	0,170675	0,17075	0,17079	0,170811

Для последнего столбца уже выполняется критерий остановки. (т.е. последовательные приближения мало отличаются друг от друг)

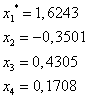
Сделаем обратную замену и запишем ответ:

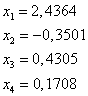
Решения, полученные разными способами совпадают.

Понравилась статья?

      Назад Оглавление