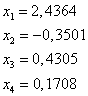Назад Оглавление Вперед

Найти решение системы 4 линейных уравнений с 4-мя неизвестными 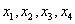с точностью до 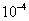методом простой итерации;

Решение:
Исходная система:

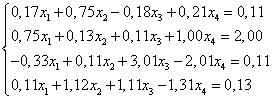
Для того, чтобы матрица была диагонально доминирующая, сделаем замену

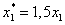
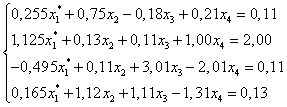
Поменяем местами строки так, чтобы элементы, стоящие на диагоналях были в строке наибольшими по модулю.

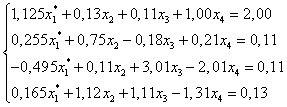
Преобразуем систему к виду

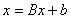
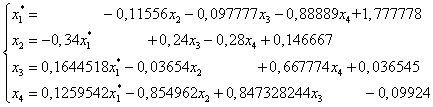
Запишем в матричной форме:

Выберем начальное приближение – столбец свободных членов, т.е.

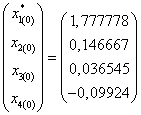
Вычислим следующее приближение

Составит таблицу приближений (в первой строке указан номер итерации)

1	2	3	4	5
1,8454667	1,5514813	1,7901222	1,6604362	1,6325299
-0,4212208	-0,4977375	-0,2479944	-0,4256629	-0,3634016
0,2572761	0,5431011	0,3039202	0,4273531	0,4398400
0,2810418	-0,0089227	0,1308173	0,1717312	0,1080851

 

6	7	8	9	10
1,6806887	1,6284165	1,6377836	1,6401013	1,6259311
-0,3330957	-0,3782005	-0,3463708	-0,3513301	-0,3576108
0,3904742	0,4375511	0,4240237	0,4208902	0,4327587
0,1683817	0,1585289	0,1532716	0,1702025	0,1635993

 

11	12	13	14	15
-0,1464119	1,6283235	1,6256322	1,6270479	1,6253628
-0,4947623	-0,3523185	-0,3516129	-0,34972 26	-0,3511343
0,3897036	0,4287323	0,4305921	0,4288624	0,4302550
0,2657379	0,1698046	0,1679156	0,1697559	0,1700847

 

16	17	18	19	20
1,6250976	1,6252166	1,6246362	1,6246362	1,6245795
-0,3503192	-0,3501635	-0,3504442	-0,3504442	-0,3501834
0,4302490	0,4300158	0,4304694	0,4304694	0,4303923
0,1698454	0,1705038	0,1704544	0,1704544	0,1707030

 

21	22	23	24	25
1,6244246	1,6243784	1,6243784	1,6243410	1,6243410
-0,3501931	-0,3501401	-0,3501401	-0,3501043	-0,3501043
0,4304984	0,4304960	0,4304960	0,4305058	0,4305058
0,1706761	0,1707768	0,1707768	0,1708025	0,1708025

Для последнего столбца уже выполняется критерий остановки. (т.е. последовательные приближения мало отличаются друг от друг)

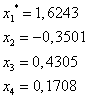
Сделаем обратную замену и получим ответ:

Понравилась статья?

      Назад Оглавление Вперед