Задача:
Найти расстояние между линиями
и используя вариационные методы.
Решение:
Для решения этой задачи требуется найти минимальное расстояние между двумя точками, одна из которых лежит на кривой , а другая – на кривой (в данном случае это прямая, но не важно).
Вспоминая формулу из математического анализа для вычисления длины участка кривой, получаем задачу вариационного исчисления:

Требуется минимизировать функционал
,
где — точка на кривой , а — точка на .
Подынтегральная функция зависит только от 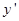. Известно, что в этом случае экстремальные кривые имеют вид .
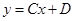Условие трансверсальности:
.
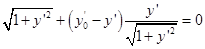Найдем производные для функций данных линий:
А)

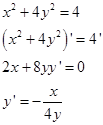
Б)

Запишем систему

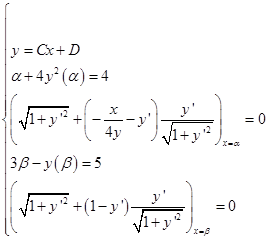
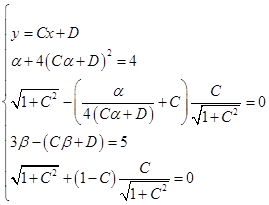
Решив эту простую систему, получим

Подставим полученные значения в функционал

Найдем наименьшее по модулю из этих двух результатов



Ответ: расстояние между линиями равно