Следующие теоремы необходимы для вычисления пределов, доказательства их можно найти в любом учебнике.
Предположим, что существуют
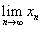и 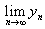, тогда верны следующие равенства:
1.
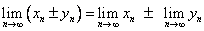
2.
3. 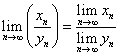, если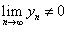
Рассмотрим несколько примеров, описывающих основные принципы вычисления пределов числовых последовательностей. Задания взяты из задачника «Сборник задач и упражнений по математическому анализу» под ред. Демидовича Б.П.
Пример:
Найти предел

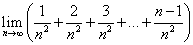
Преобразуем общий вид элемента последовательности:

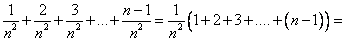
Вынесли общий множитель за скобки. При этом в скобках получилась сумма последовательных целых чисел от 1 до 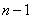. Её можно понимать как сумму арифметической прогрессии, первый элемент которой 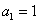, разность 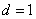, количество членов 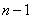. Со школьной скамьи большинству россиян известно, что сумма арифметической прогрессии равна «первый элемент пляс последний, умножить на количество элементов и поделить пополам».

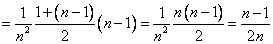
Итак, предел принял вид:

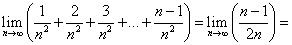
Далее следует сделать стандартное действие:
«Если переменная стремится к бесконечности, а в числителе и знаменатели стоят либо многочлены, либо выражения, связанные со степенями, то следует разделить числитель и знаменатель на переменную в максимальной из присутствующих степеней.»
В этом пределе 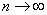, в числителе и знаменателе стоят многочлены, максимальная из имеющихся степеней – первая. Поделим числитель и знаменатель на

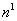
Золотое правило: всегда пытаться подставить в исследуемое выражение то, к чему стремиться переменная.

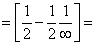
Очевидно, что 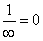, т.е. предел вычислен

Ответ: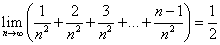
Проанализируем сделанное:
а) вынесли общий множитель за скобки,
б) вспомнили про арифметическую прогрессию и нашли ее сумму, (это основная фишка задачи)
в) разделили числитель и знаменатель на ,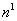
г) известно, что .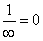

Пример:
Найти предел

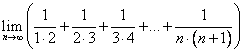
Преобразуем общий вид элемента последовательности:

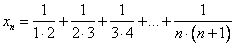
Обратим внимание на то, что в знаменателе стоят произведения. Это намек. Рассмотрим последнее слагаемое (т.к. это общий вид всех слагаемых):

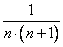
Представим эту дробь в виде суммы двух дробей. Числители этих добей можно находить с помощью «метода неопределенных коэффициентов», а можно и «методом пристального взгляда»

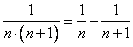
Так можно преобразовать каждое слагаемое:

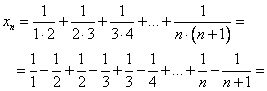
Особенность полученного выражения в том, что каждое слагаемое распадается на разность двух дробей, причем та, что идет с минусом в следующем слагаемом будет с плюсом, т.е., после приведения подобных, получаем:

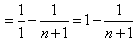
Вернемся к вычислению предела:

Ответ: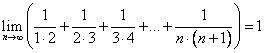
Проанализируем сделанное:
а) Разложили каждое слагаемое на разность двух дробей, (это основная фишка задачи)
б) привели подобные
в) известно, что 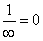.