Еще один из типов задач на движение — это когда кто-то кого-то догоняет, желательно даже не одного, а двух.
Здесь будет разобрано решение подобной задачи с применением временных осей.
Задача:
Из пункта А выехал грузовой автомобиль со скоростью 40 км/ч. Через час по той же дороге и в том же направлении выехал еще один грузовой автомобиль, но со скоростью 50 км/ч. Еще через час по той же дороге и в том же направлении выехал легковой автомобиль. Легковой автомобиль догонит первый грузовик через 21 минуту после того, как он догонит второй грузовик.
Чему равна скорость движения легкового автомобиля?
Решение:
План: В этой задаче за переменную будем брать скорость, а уравнение будем составлять относительно пройденного расстояния, т.к. легковушка догоняет других, т.е. пройденные расстояния в момент встречи равны.
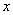 км/ч – скорость движения легкового автомобиля.
км/ч – скорость движения легкового автомобиля.
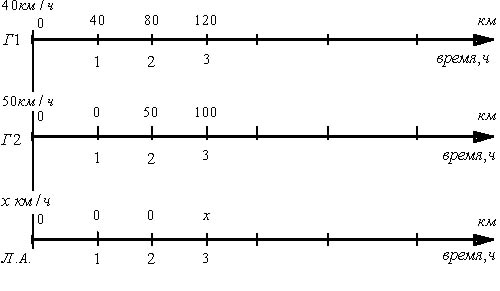
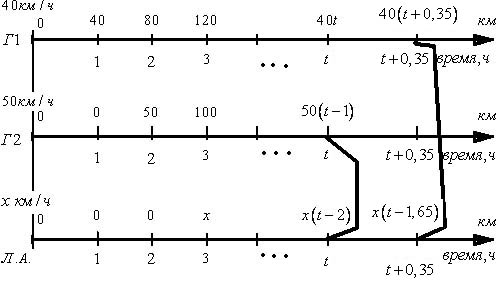
Для решения этой задачи каждому из автомобилей поставим в соответствие временную ось, подписывая над каждым делением этой оси количество километров, которое прошла машина от пункта А.
Составим схему. Первая ось соответствует первому грузовому автомобилю. Вторая – второму, третья – легковому. В момент запуска секундомера у всех проехано ноль километров:
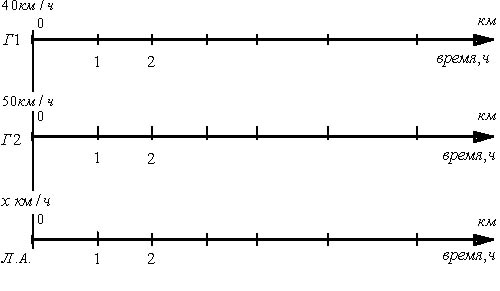
Первый автомобиль поехал, а второй пока стоит. К исходу первого часа ситуация меняется – первый уже проехал 40 км, а второй грузовик сейчас стартует, а третий участник движения пока стоит на месте:
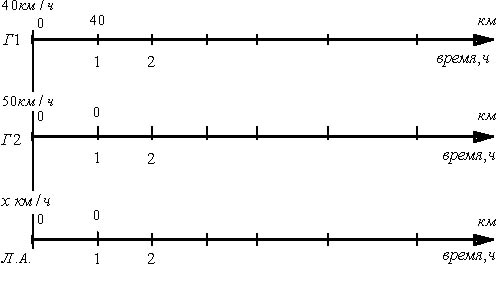
Через час после выезда первого (после начала отсчета времени) выезжает второй грузовик, и к исходу второго часа ситуация такова:
А) первый двигался 2 часа со скоростью 40 км/ч, т.е. прошел 80 км.
Б) второй двигался 1 час со скоростью 50 км/ч, т.е. прошел 50 км.
В) третий начнет движение.
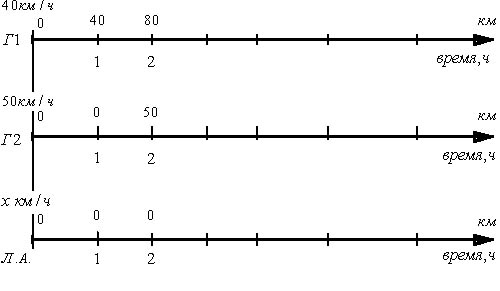
Прошел еще час:
Итак, машины едут, спидометры накручивает километры, часы тикают. Проходит какое-то время и легковой автомобиль догоняет второй грузовик. Пусть это произойдет через  часов с момента запуска секундомера, т.е. с момента старта первого грузовика. На этот момент:
часов с момента запуска секундомера, т.е. с момента старта первого грузовика. На этот момент:
А) первый двигался  часов со скоростью 40 км/ч, т.е. прошел
часов со скоростью 40 км/ч, т.е. прошел  километров.
километров.
Б) второй двигался 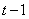 часов (он выехал через час после первого) со скоростью 50 км/ч, т.е. прошел
часов (он выехал через час после первого) со скоростью 50 км/ч, т.е. прошел 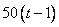 километров.
километров.
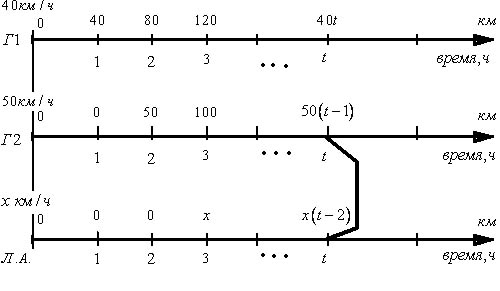
В) третий двигался 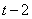 часа (он выехал через два часа после первого) со скоростью
часа (он выехал через два часа после первого) со скоростью 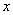 км/ч, т.е. прошел
км/ч, т.е. прошел 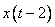 километров.
километров.
Ключевое: Третий догнал второго (на схеме это обозначено соединением этих двух временных точек ломаной линией. Ломаная она исключительно для того, чтобы не проходить по тексту и не закрывать его.), а значит расстояние, пройденное ими одинаковое. Составим уравнение:
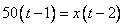 .
.
Поехали дальше.
Легковой автомобиль догонит первый грузовик через 21 минуту после того, как он догонит второй грузовик (не забудем перевести 21 минуту в часы — 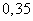 часа):
часа):
А) первый двигался 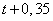 часов со скоростью 40 км/ч, т.е. прошел
часов со скоростью 40 км/ч, т.е. прошел 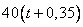 километров.
километров.
Б) второй грузовик уже не важен.
В) третий двигался 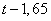 часа со скоростью км/ч, т.е. прошел
часа со скоростью км/ч, т.е. прошел 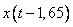 километров.
километров.
Ключевое: Третий догнал первого, а значит расстояние, пройденное ими одинаковое. Составим уравнение:
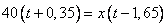
Получили систему из двух уравнений и двух неизвестных. Запишем и решим её.
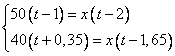
Выразим 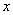 из первого уравнения и подставим во второе:
из первого уравнения и подставим во второе:

Подставим в выражение для 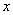 :
:

Ответ: Скорость легкового автомобиля 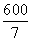 или 90 км/ч.
или 90 км/ч.
Вывод.
Такое графическое представление всех движущихся объектов наглядно показывает пройденные объектами расстояния и время движения, что облегчает составление уравнений. Более короткий метод решения аналогичных задач рассмотрен на следующей странице.


