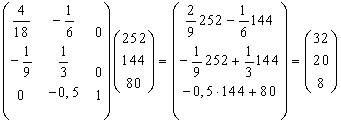Оглавление:
1.Симплекс-метод.
2.Графический метод.
3.Двойственная задача линейного программирования.
4.Задача о «расшивке узких мест производства».
Постановка задачи:
Предприятие выпускает 4 вида изделий, имея 3 группы оборудования. Нормы времени на обработку каждого изделия на каждой группе оборудования заданы матрицей А, фонд времени работы каждой группы оборудования задан матрицей В. Требуется составить такой план производства, при котором прибыль предприятия будет наибольшей.
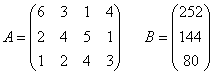
Прибыль на единицу изделия соответствующей группы задана матрицей:
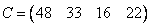
Обозначим за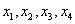 
— планируемое количество единиц изделий каждого типа.
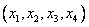— искомый план.
Его компоненты должны удовлетворять условию, что суммарное время обработки всех изделий на данной группе оборудования не должно превышать фонда времени работы этой группы оборудования. Запишем это ограничение в виде системы.
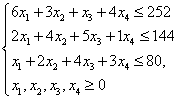
Целевая функция, т.е. прибыль от выполнения плана 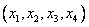равна:
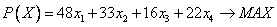
Прибыль должна быть максимальна.
Получена задача на условный экстремум. Для ее решения систему неравенств при помощи дополнительных неотрицательных переменных заменим системой линейных алгебраических уравнений.
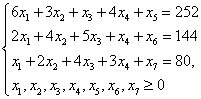
Определим начальный план:
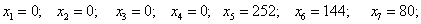
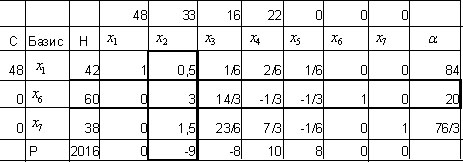
Первые четыре компоненты говорят о том, что ничего не производится и получена нулевая прибыль. Занесем данные в симплекс таблицу:
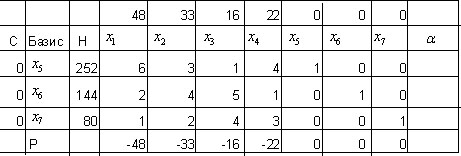
Выберем в последней строке, отвечающей за план наибольшее по модулю отрицательное число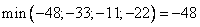 
, т.е. первый столбец. Занесем в столбец 
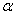значения, равные отношению элементов столбца H к элементам первого столбца 
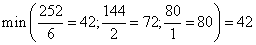, выберем среди них наименьшее значение. Пересечение этой строки и первого столбца даст нам разрешающий элемент 6.
Введем в базис переменную вместо и пересчитаем элементы таблицы по методу прямоугольников
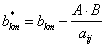
и повторим итерацию:
, 
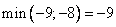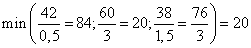
В этот раз в базис входит переменная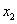 
, вместо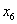 
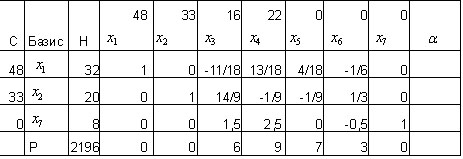
В последней строке отсутствуют отрицательные элементы, значит полученный план
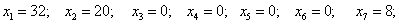оптимальный и
.
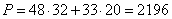Этот план предусматривает остатки ресурсов третьего типа в размере 8 единиц.
Вывод: для максимальной выручки в размере 2196 следует выпускать продукцию первого типа в объеме 32 шт, второго типа – 20 шт., при этот остатки ресурсов третьего типа составят 8 единиц.
Проверим соотношение H=Q-1B
