Задача: На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 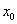 . Найдите значение производной функции
. Найдите значение производной функции 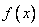 в точке
в точке 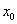 .
.
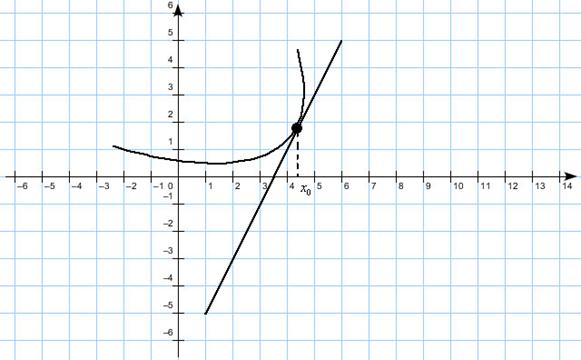
Решение:
Помним, что производная равна тангенсу угла наклона касательной (т.е. угловому коэффициенту касательной)
Касательная есть, осталось найти тангенс её наклона к положительному направлению оси абсцисс.
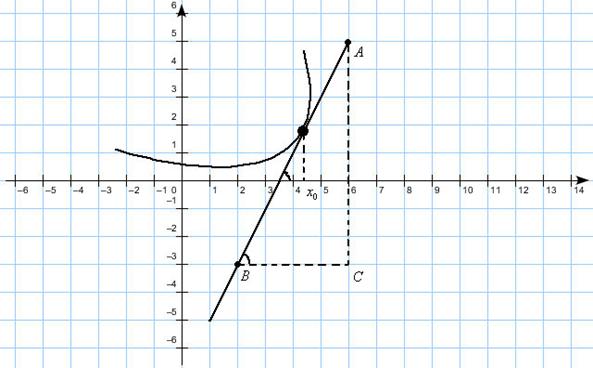
Требуется изобразить какой-либо прямоугольный треугольник, в котором касательная была бы гипотенузой, а вершины лежали бы в узлах сетки.
Например, вот такой треугольник:
Угол для исследования :
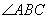 .
.Известно, что тангенс угла в прямоугольном треугольнике равен отношению длины противолежащего катета к длине прилежащего.
Считаем клеточки, и получаем, что:
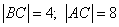 .
.Итого:
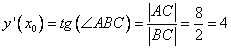
Ответ: Производная в этой точке равна 4.
Задача: На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 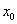 . Найдите значение производной функции
. Найдите значение производной функции 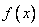 в точке
в точке 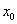 .
.
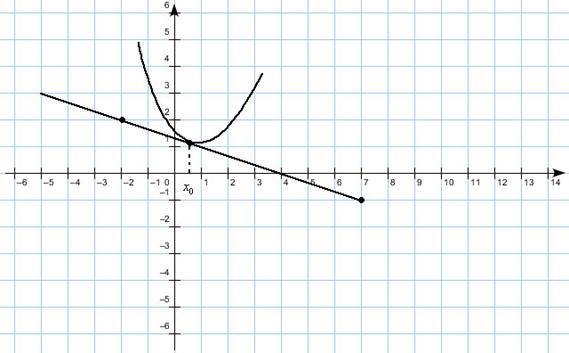
Решение:
Замечание: Задача аналогична предыдущей с тем отличием, что касательная «наклонена влево» и мы понимаем, что её угловой коэффициент отрицателен.
Замечание: Нужные точки касательной, точно расположенные в узлах координатной решетки, как бы невзначай обозначены жирненькими точками. Их то мы и возьмем за вершины треугольника.
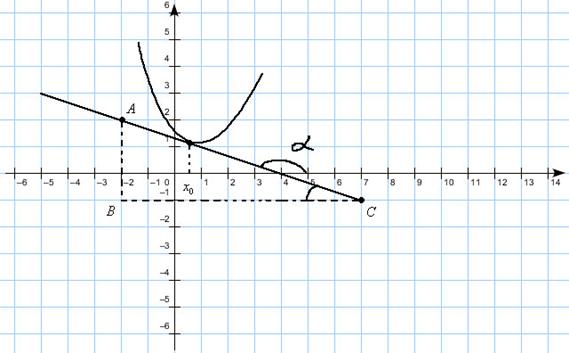
Требуется найти 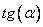 . Из чертежа видно, что
. Из чертежа видно, что 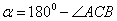 .
.
А из тригонометрии известно, что 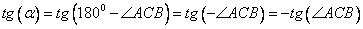
Считаем клеточки, и получаем, что:
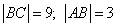 .
.Итого:
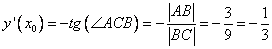
Ответ: Производная в этой точке равна
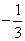 .
.


