Задача: Прямая  является касательной к графику функции
является касательной к графику функции 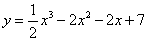 . Определить координаты точки касания.
. Определить координаты точки касания.
Решение:
Замечание 1: Производная функции 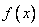 в точке
в точке 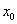 равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции  , проведенной в точке
, проведенной в точке 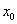 .
.
Угловой коэффициент прямой  равен -4. Вычислим производную функции
равен -4. Вычислим производную функции 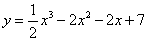 и приравняем их.
и приравняем их.


Вывод:  — абсциссы точек, в которых касательная к графику
— абсциссы точек, в которых касательная к графику 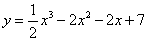 имеет угловой коэффициент, равный -4.
имеет угловой коэффициент, равный -4.
Известно, что касательная задана уравнением  . Найдем координаты точек пересечений этой прямой и кубической параболы.
. Найдем координаты точек пересечений этой прямой и кубической параболы.

Совпадает точка
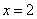 , т.е. это и есть абсцисса точки касания. Вычислим ординату. Удобнее конечно подставлять в линейную функцию, чем в кубическую, результат то одинаков, ведь точка касания принадлежит как кривой так и касательной.
, т.е. это и есть абсцисса точки касания. Вычислим ординату. Удобнее конечно подставлять в линейную функцию, чем в кубическую, результат то одинаков, ведь точка касания принадлежит как кривой так и касательной.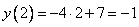
Ответ: точка качания имеет координаты 



