Задача: Прямая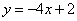 
параллельна касательной к графику функции 
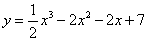. Определить абсциссу точки касания.
Решение:
Замечание 1: Угловые коэффициенты параллельных прямых равны.
Известно, что касательная к графику функции 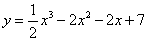параллельна прямой 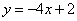, т.е. угловые коэффициенты касательной и этой прямой равны между собой, т.е. 
.
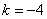Замечание 2 (геометрический смысл производной): Производная функции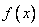 
в точке 
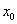равна угловому коэффициенту касательной к графику функции 
, проведенной в точке .
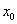Вычислим производную:
Выше выяснили, что угловой коэффициент равен -4, т.е. производная равна -4.
Вывод: 
— абсциссы точек, в которых касательная к графику 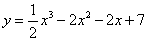параллельна прямой .
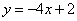Ответ:
Проиллюстрируем эту задачу графиком, хотя при её решении график строить необходимости нет.
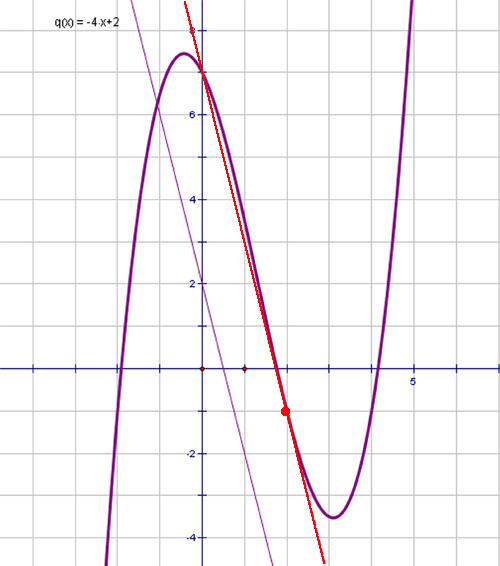
Касательная – линия красного цвета, точка касания 
, и она, конечно же, параллельна данной прямой.