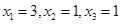Метод Гаусса для решения систем линейных алгебраических уравнений заключается в следующем:
Дано: Решить систему уравнений методом Гаусса:
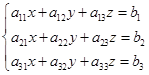
Запишем расширенную матрицу системы:
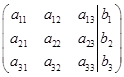
И линейными алгебраическими преобразованиями приводим эту матрицу сначала к верхнетреугольному виду (прямой путь):
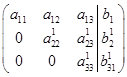
Потом к диагональному виду (обратный путь):
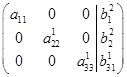
И к такому виду, чтобы в правой части этой матрицы стояла единичная:
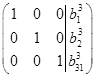
Тогда решением системы будет:
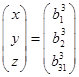
Замечание: этот метод можно применять к системам любой размерности.
Пример:
Решить методом Гаусса систему уравнений:
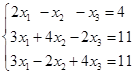
(Д.К. Фаддеев, И.С. Соминский, Задачи по высшей алгебре, № 400, а )
Решение:
Составим расширенную матрицу системы
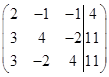
От элементов третьей строки отнимем элементы второй строки (III +II(-1) )
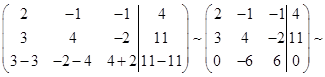
Умножим элементы первой строки на -3, а второй на 2 ( -3*I; 2*II )
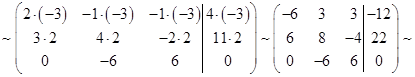
Прибавим к элементам второй строки элементы первой ( II+I )
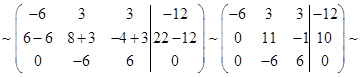
Поделим третьей строки на -6 ( III:(-6) )
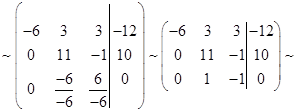
Поменяем для удобства вторую и третью строки местами
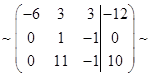
Прибавим к третьей строке элементы второй, умноженные на -11 (III+II(-11) )
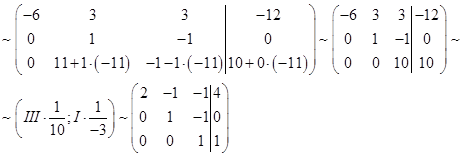
Матрица коэффициентов приведена к верхнетреугольному виду, т.е. прямой ход закончен.
Сделаем обратный ход, теперь пойдем не «сверху вниз», а «снизу вверх»
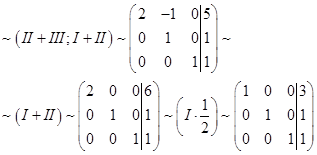
Все, обратный ход также закончен, в левой части матрицы стоит единичная, запишем ответ:
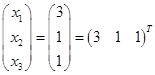
Или просто:
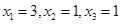
Ответ: