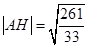Пример 1.
Найти векторное произведение векторов, заданных своими координатами:
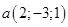 и
и 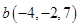 .
.Решение:
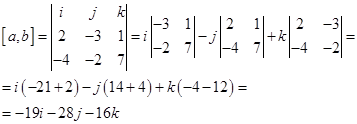
Т.е. получили вектор с координатами 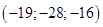
Ответ: 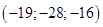
Пример 2.
Упростить выражение:
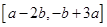
Решение:
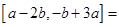
Используем свойство:
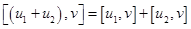
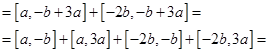
Используем свойство:
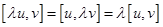
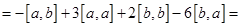
Свойство:
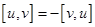
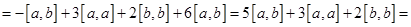
Используем первое свойство о том, что векторное произведение коллинеарных векторов равна 0, т.е.
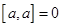 и
и 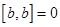
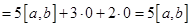
Ответ:
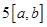
Пример 3.
Даны три точки:
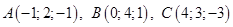 . Найти площадь треугольника ABC. Найти длину высоты, опущенной из вершины А.
. Найти площадь треугольника ABC. Найти длину высоты, опущенной из вершины А.Решение:
Среди формул для вычисления площади треугольника давайте выберем вот эту:
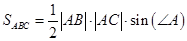
И, о чудо, видим произведение длин двух отрезков (что то же самое, что произведение длин двух векторов) на синус угла между ними. Что равно длине вектора-результата векторного произведения векторов
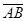 и
и 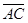 .
.Найдем координаты этих векторов:
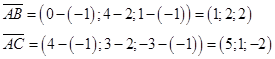
И вычислим площадь:
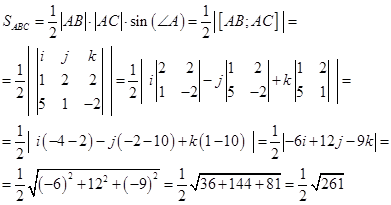
Площадь треугольника равна
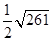
Найдем длину высоты, опущенной из вершины А.
Для этого вспомним еще формулы для вычисления площади треугольника. Например ту, где говорится «площадь треугольника равна половине произведения высоты на основание».
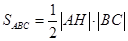 .
.Известны координаты точек В и С, т.е. можно вычислить длину стороны ВС. Известна так же площадь треугольника. Подставим данные.
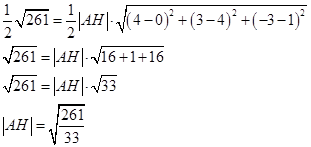
Ответ:
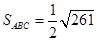 ;
;