Оглавление.
1. Скалярное произведение векторов.
2. Скалярное произведение через координаты, вычисление угла между векторами.
3. Примеры решения задач на тему «Скалярное произведение».
4. Векторное произведение.
5. Свойства векторного произведения.
6. Примеры решения задач на тему «Векторное произведение».
Напомним для начала определение вектора:
Определение:
Рассмотрим любые две точки А и В в пространстве. Вектором 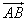 называется направленный отрезок, соединяющий точки А и В, при этом в точке А будет лежать начало этого отрезка (точка приложения вектора), а в точке В – конец.
называется направленный отрезок, соединяющий точки А и В, при этом в точке А будет лежать начало этого отрезка (точка приложения вектора), а в точке В – конец.
Два вектора 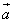 и
и 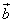 , расположенные в произвольных точках пространства считаются равными, если их можно совместить параллельным переносом.
, расположенные в произвольных точках пространства считаются равными, если их можно совместить параллельным переносом.
Все равные между собой вектора называются свободным вектором, и, по сути считаются одном и тем же математическим элементом, т.е. если векторы равны, но расположены в разных точках пространства, то это, на самом деле, один и тот же вектор.
О том, как складывать, вычитать вектора, умножать их на число, исследовать на линейную зависимость-независимость будет рассказано в другой статье. Здесь хочется поговорить об особой операции между двумя векторами, в результате которой получается число. Да-да, пусть вас не пугает то, что какое-то действие производиться с объектами одно природы (векторами), а в результате получается объект другой природы (действительное число).
Определение скалярного произведения векторов:
Скалярным произведением двух векторов 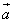 и
и 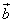 называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 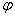 между ними. Обозначение:
между ними. Обозначение:
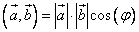 .
.Замечание: В некоторой литературе встречается иное обозначение скалярного произведения: 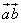 .
.
Свойства:
1) 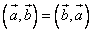 — свойство переместительности.
— свойство переместительности.
2) Скалярное произведение двух ненулевых векторов 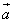 и
и 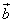 равно нулю тогда, и только тогда, когда эти векторы перпендикулярны между собою.
равно нулю тогда, и только тогда, когда эти векторы перпендикулярны между собою.
3) Скалярное произведение ненулевого вектора на самого себя равно квадрату длины этого вектора: 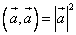 .
.
4) Скалярное произведение двух векторов 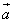 и
и 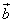 равно произведению длины вектора
равно произведению длины вектора 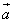 на длину проекции вектора
на длину проекции вектора 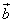 , опущенной на вектор
, опущенной на вектор 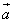 .
.
Это свойство не слишком очевидно, а потому:
Доказательство:
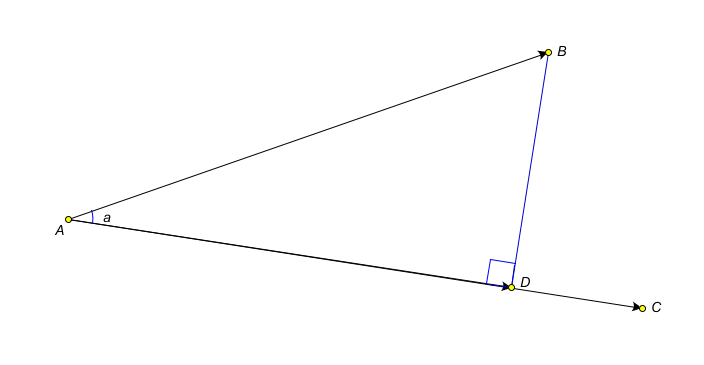
Даны векторы 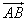 и
и 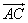 , угол между ними составляет a радиан. Требуется вычислить скалярное произведение этих векторов:
, угол между ними составляет a радиан. Требуется вычислить скалярное произведение этих векторов:
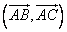 .
.По определению скалярного произведения:
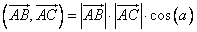
Рассмотрим прямоугольный треугольник
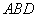 . Всем известно, что в прямоугольном треугольнике косинус острого угла равен отношению прилежащего катета к гипотенузе. Запишем сей факт для этого треугольника:
. Всем известно, что в прямоугольном треугольнике косинус острого угла равен отношению прилежащего катета к гипотенузе. Запишем сей факт для этого треугольника:
И проведем преобразования:
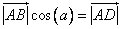 .
.Подставим полученное выражение в скалярное произведение:
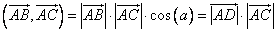 .
.Заметим, что
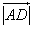 и есть длина проекции вектора
и есть длина проекции вектора 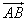 на вектор
на вектор 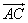 .
.Свойство доказано.
Замечание: Конечно же, при вычислении скалярного произведения векторов 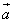 и
и 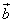 не важно, проецировать ли
не важно, проецировать ли 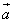 на
на 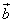 или
или 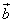 на
на 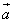 .
.
5) 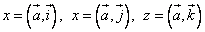
— координаты любого вектора 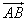 в прямоугольной системе координат равны скалярным произведениям этого вектора на орты осей координат.
в прямоугольной системе координат равны скалярным произведениям этого вектора на орты осей координат.
6) 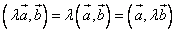
Числовой множитель можно выносить за знак скалярно произведения.
7) 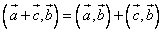
— свойство дистрибутивности относительно сложения.
Итак, перечислены свойства, которыми обладает скалярное произведение. С помощью них можно доказать и вывести еще одну формулу для вычисления скалярного произведения и формулу для вычисления угла между векторами, координаты которых известны.


