Термин «произведение» для векторов требует обязательного дополнения. Или это скалярное произведение, или векторное, или смешанное.
В этой статье разбирается векторное произведение векторов.
Помним, что результатом скалярного произведения вектором является скаляр, т.е. число. Логично предположить, что результатом векторного произведения векторов является вектор.
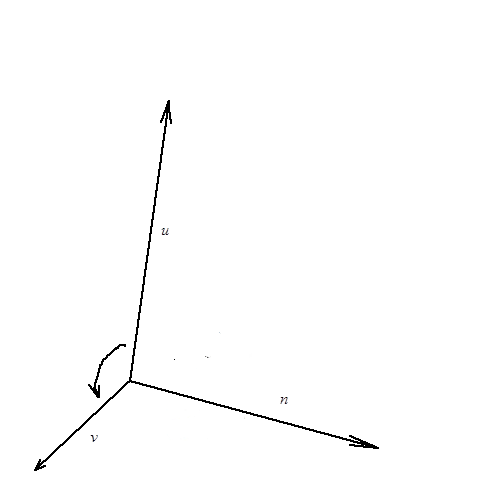
Определение (Александров П.С., Лекции по аналитической геометрии.): Векторным произведением вектора u на вектор v называется вектор n,
модуль которого равен произведению модулей векторов u и v на синус угла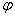 
между ними: 
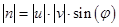. Этот вектор перпендикулярен к плоскости 
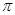, в которой лежат векторы u и v, если их отложить от одной точки. Он направлен так, что упорядоченная тройка векторов u,v,n имеет положительную ориентацию.
Обозначение: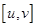 
или 
.
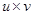Координаты вектора-результата векторного произведения векторов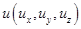 
и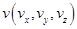 
вычисляется по формуле:
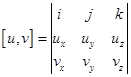
Замечание: Правило буравчика для определения направления результата векторного произведения.
Пусть требуется найти векторное произведение . Совместим параллельным переносом вектора так, чтобы они исходили из одной точки.
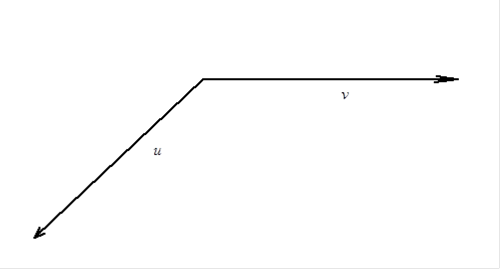
Представим, что держим в правой руке штопор,
так что его ручка параллельна первому вектору произведения.
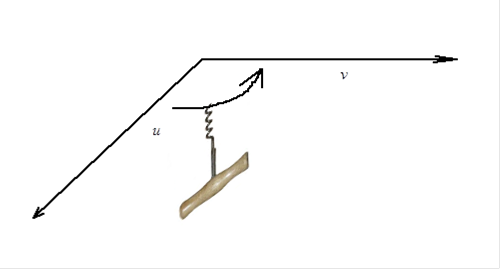
Теперь нужно повернуть штопор по кратчайшему пути так, чтобы его ручка стала параллельна второму вектору произведения, т.е. он будет «закручиваться» или «выкручиваться».
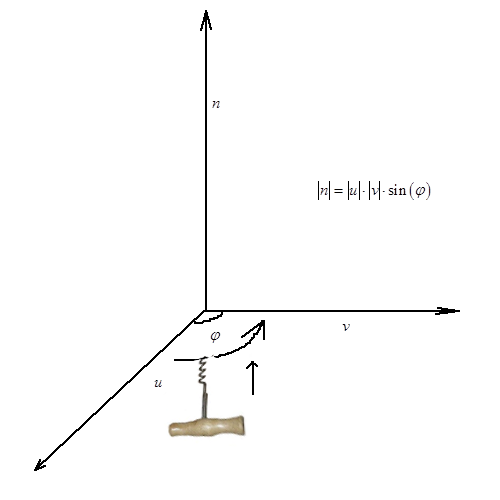
Вектор-результат векторного произведения будет направлен в ту сторону, в которую двинется острие штопора.
Другой вариант расположения:
