Уравнение вида
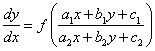(1)можно свести к однородному типу.
Общий вид преобразований.
Для того, чтобы привести уравнение (1) к однородному типу дифференциальных уравнений надо составить систему вида:
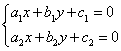
Первый случай.
Эта система имеет решение.
Пусть решение этой системы :
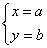.Тогда, для приведения уравнения (1) к однородному типу необходимо сделать подстановку вида
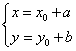
Пример 1:
Найти общий интеграл уравнения
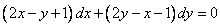
Решение:
Составим систему
Попробуем решить эту систему:
Сделаем замену:
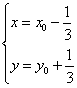
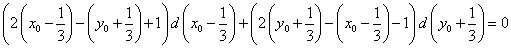
Раскроем скобки и приведем подобные. Помним, что
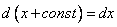
Полученное уравнение есть дифференциальное уравнение однородного типа. Решим его.
Замена
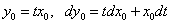
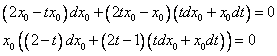
Поделим обе части уравнения на
.
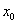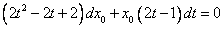
Получили уравнение с разделяющимися переменными.
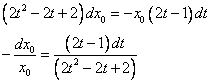
Проинтегрируем обе части уравнения
Сделаем обратные замены:
И еще одну:
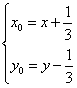
Преобразуем полученное выражение для красоты. Т.е. сделаем дроби максимум двухэтажными.
Ответ:
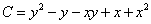
Второй случай.
Напомним. Уравнение
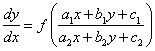
Приводим к однородному типу, составили систему
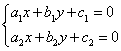,а решений эта система не имеет.
В этом случае следует сделать замену
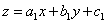. Нечто подобное делалось в разделе «Уравнения, сводящиеся к уравнению с разделяющимися переменными».Пример 2:
Найти общий интеграл уравнения:
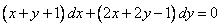
Решение:
Составим систему
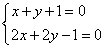
Попробуем решить эту систему:
В ходе решения получили, что второе уравнение системы не является верным равенством ни при каких значениях переменной, значит, и вся система не имеет решения.
Делаем замену:
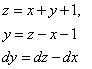
Замечание: В уравнении должны остаться только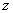 
, как функция, зависящая от 
, и сам .
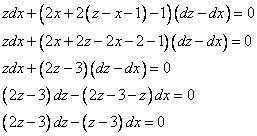
Получили уравнение с разделяющимися переменными.
Замечание: В этом подслучае не переходим к уравнению однородного типа, а сразу к типу «уравнение с разделяющимися переменными».
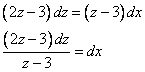
Проинтегрируем обе части уравнения.
Сделаем обратную замену: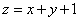 
.
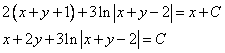
Ответ: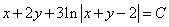 
.