Вперед

Оглавление.

1. Дифференциальные уравнения с разделяющимися переменными.
2. Однородные дифференциальные уравнения.
3. Дифференциальные уравнения, сводящиеся к однородным.
4. Линейные однородные уравнения с постоянными коэффициентами.
5. Решение неоднородного линейного уравнения с постоянными коэффициентами и специальной правой частью.1.

Дифференциальные уравнения с разделяющимися переменными.

Общий вид:
Уравнениями с разделяющимися переменными называются дифференциальные уравнения, которые можно записать в видах:
а)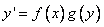
б) .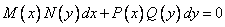
Для того, чтобы решить уравнение этого типа необходимо провести такие алгебраические преобразования, чтобы в одну часть уравнения (левую или правую часть равенства) входило только 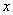, а в другую только 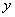. Причем сомножители 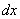и 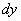должны стоять в числителях.
После преобразований следует проинтегрировать обе части полученного равенства.

Общий вид преобразований:
а)

Замечание: Произведено деление на 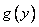, т.е. частный случай, когда 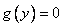следует рассмотреть отдельно ( это следует сделать обязательно, иначе ответ будет неполным).

Проинтегрируем полученное выражение.

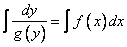
Вычислив эти интегралы, получаем решение дифференциального уравнения.

б)
.
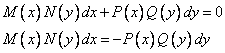Предположим, что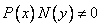

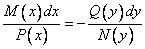
Проинтегрируем полученное выражение.

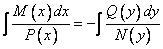
Вычислив эти интегралы, получаем решение дифференциального уравнения.

Пример 1:
Решить дифференциальное уравнение

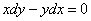
Решение:

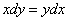
1)
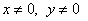
Разделим обе части равенства на .

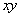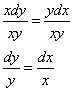
Переменные разделены. Проинтегрируем обе части уравнения.

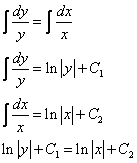
Замечание: При решении дифференциальных уравнений отдельное внимание следует уделять константам. Например, в этом случае 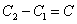(константа минус константа равно константа).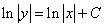

Замечание: Продолжаем работать с константой: 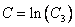(константу можно представить как логарифм натуральный от константы).

Итог случая:
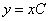
Замечание: В итоговом равенстве не указан индекс у константы. Он не нужен, потому, что не важно, как её обозначить, 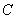или 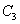, это просто любая константа.
2) Не забываем рассмотреть случай, когда 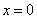или .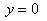
2а)
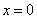
Подставляем в исходное уравнение:

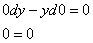
— равенство верно при любом .
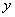Итог случая: 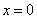, 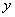— любое
2б)
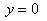
Подставляем в исходное уравнение:

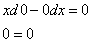
— равенство верно при любом .
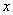Итог случая: 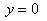, 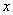— любое

Ответ: , .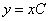
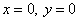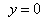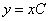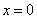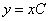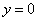Замечание: один из ответов достигается в случае при С = 0, т.е. отдельно не нужно его выносить, а вот с так не получиться, т.к. если подставлять в , то , а 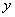должно быть любое.
Ответ (окончательный): , .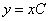

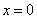Пример 2:

Решить дифференциальное уравнение

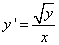
Решение:
Замечание: Всегда в этом случае нужно помнить, что 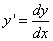. Следует заметить, что, так как в знаменателе не может стоять нуля, то 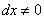, то есть, в этом уравнении, .

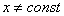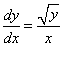
1)

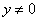
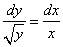
Переменные разделены. Проинтегрируем обе части уравнения.

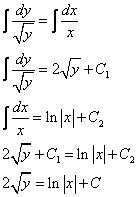
Вообще говоря, это выражение уже является решением исходного дифференциального уравнения, так как в нем (последнем равенстве) не содержится производных, дифференциалов и интегралов. Однако это выражение еще можно преобразовать для красоты (и тренировки обращения с константами).

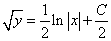
Конечно же 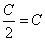. Это равенство грубо с точки зрения математики, однако его следует читать как «половина произвольной константы также произвольная константа» и все встает на свои места.

.

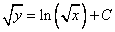
И снова константы: .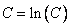

Итог случая: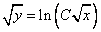
2)
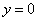
Подставим в исходное уравнение:

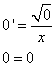
Равенство верно при 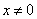, а это уже обсуждалось в первом случае задачи.
Итог случая: 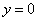при любых .
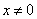Ответ: , .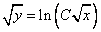

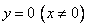Уравнения, приводящееся к типу «уравнение с разделяющимися переменными».

Уравнение вида 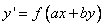при помощи замены 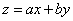становиться уравнением с разделяющимися переменными.

Замечание: Многие из типов дифференциальных уравнений заменами или преобразованиями приводятся к типу «уравнение с разделяющимися переменными».
Замечание: Следует понимать, что в результате замены в уравнении должны остаться только независимая переменная 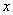и зависимая от нее переменная .

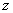Общий вид преобразований:

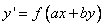
Замена: .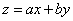
Выразим из этого равенства : .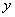
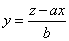Найдем выражение для 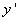(по правилу дифференцирования сложной функции ): .
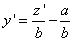Подставим в исходное равенство:

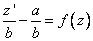
Получили уравнение с разделяющимися переменными. Разделим их.

Переменные разделены, проинтегрируем обе части равенство и получим решение исходного дифференциального уравнения (рассмотрен общий вид уравнения, в котором ).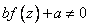

Пример 3:
Решить дифференциальное уравнение

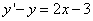
Решение:
Приведем уравнение к виду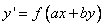

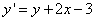
Замена: .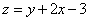
Выразим из этого равенства : .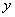
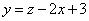Найдем выражение для :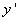
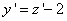
Подставим в исходное равенство:

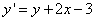
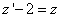
Получили уравнение с разделяющимися переменными. Разделим их.

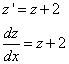
1)

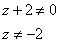
Поделим обе части уравнения на :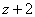

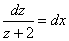
Проинтегрируем обе части равенства:

Сделаем обратную замену :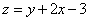

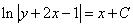
Итог случая: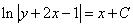
Преобразуем выражение «для красоты»:

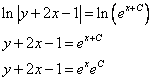
Помним, что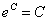

Итог случая (окончательный):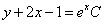

2)
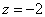
Подставим в исходное уравнение (после замены):

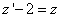
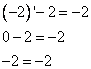
Равенство верное, 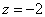является решением. Сделаем обратную замену :

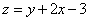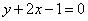
Итог случая: .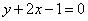
Замечание: Этот ответ не стоит выделять в отдельное производство, т.к. он получается в первом случае 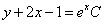при .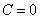
Ответ:

Понравилась статья?

Вперед