Итак, как решать однородные дифференциальные уравнения с постоянными коэффициентами мы разобрались в предыдущей статье. Разберем случай, когда правая часть ненулевая, а некоего специального вида.
Рассмотрим уравнение вида:
.
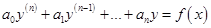Тогда решение этого уравнения будет состоять из двух частей: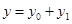 
, где 
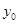— общее решение однородного уравнения 
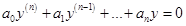, а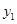 
— частное решение неоднородного уравнения.
Случай 1.
Пусть правая часть имеет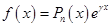 
, где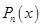 
— многочлен степени n, тогда общий вид частного решения неоднородного уравнения имеет вид: 
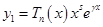, где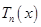 
— общий вид многочлена степени n с неопределенными коэффициентами, s равно кратности корня характеристического уравнения 
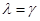, т.е., если такого корня нет, то 
.
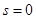Коэффициенты многочлена 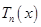определяются по методу неопределенных коэффициентов после подстановки 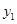в исходное уравнение.
Пример 1.
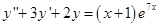
Найдем 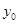, общее решение уравнения 
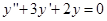при помощи характеристического уравнения.
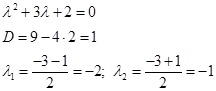
Тогда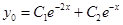 
Найдем 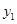по виду правой части.
Правая часть имеет вид: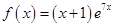 
.
Здесь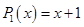 
— многочлен первой степени, 
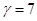, таких корней характеристического уравнения нет, т.е. .
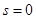Тогда частное решение неоднородного уравнения будет иметь вид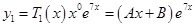 
:
Найдем производные этой функции первого и второго порядка и поставим в исходное уравнение.
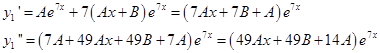
Подставим в уравнение:
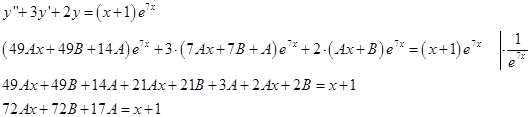
Приравняем коэффициенты при соответствующих степенях х в разных частях равенства (метод неопределенных коэффициентов:
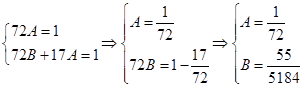
И частное решение имеет вид:
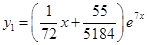
Составим ответ: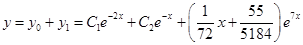 
Ответ: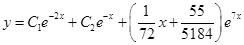 
Пример 2.
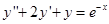
Найдем 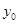, общее решение уравнения 
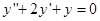при помощи характеристического уравнения.
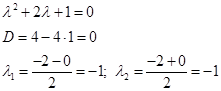
Получили действительный корень кратности 2.
Тогда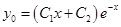 
Найдем 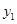по виду правой части.
Правая часть имеет вид: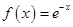 
.
Здесь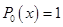 
— многочлен нулевой степени, 
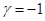, таких корней характеристического уравнения аж целых два, т.е. 
.
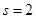Тогда частное решение неоднородного уравнения будет иметь вид :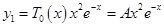 
Найдем производные этой функции первого и второго порядка и поставим в исходное уравнение.
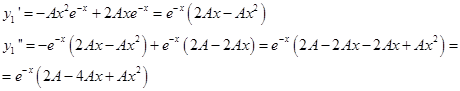
Подставим в уравнение:
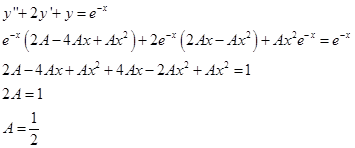
И частное решение имеет вид: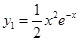
Составим ответ: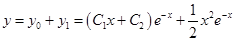 
Ответ: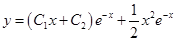 
О том, как составлять частное решение для уравнений с тригонометрической правой частью специального вида читайте далее…