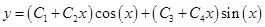Уравнение вида
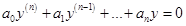
называется однородным линейным уравнением с постоянными коэффициентами. Его решение составляется на основе корней характеристического уравнения.
Этому однородному уравнению соответствует характеристическое уравнение:
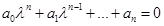, и пусть оно имеет корни
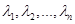, тогда:1) Если
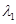— действительный корень кратности 1, то ему соответствует слагаемое общего решения вида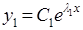 
2) Если
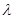— действительный корень кратности k, то ему соответствует слагаемое общего решения вида 
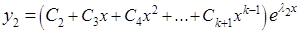, где 
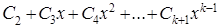— многочлен (с неопределенными коэффициентами) степени на 1 меньше кратности корня, т.е. например, если корень 
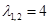, то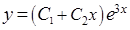 
3) Если
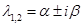— пара сопряженных комплексных корней, то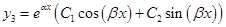 
4) Если
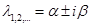— комплексно сопряженные корни кратности k, тогда, соответственно, перед косинусом и синусом пишутся не просто константы, а многочлены степени k-1.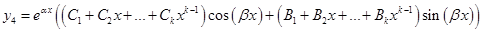
Примеры:
Пример 1.
Решить уравнение:
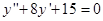
Составим и решим характеристическое уравнение
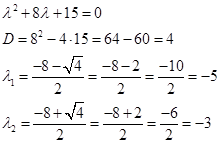
Получили два действительных корня кратности 1 ( т.е. их по 1 шт. ), тогда общее решение однородного уравнения будет иметь вид:
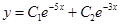
Ответ: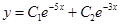
Пример 2.
Решить уравнение:
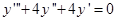
Составим и решим характеристическое уравнение
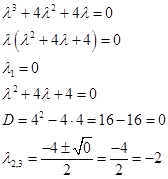
Получили три действительных корня.
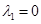( кратность- 1) и 
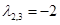(т.к. их 2 шт. одинаковых, то кратность — 2) , тогда общее решение однородного уравнения будет иметь вид:
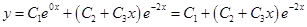
Заметьте, т.к. корень -2 имеет кратность 2, то сомножителем в соответствующем слагаемом будет не просто С, а общий вид многочлена первой степени, т.е. степени, на 1 меньшей кратности корня.
Ответ: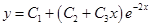 
Пример 3.
Решить уравнение:
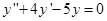
Составим и решим характеристическое уравнение
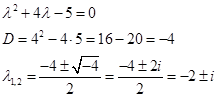
Получили пару комплексных сопряженных корней, кратности 1
, тогда общее решение однородного уравнения будет иметь вид:
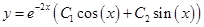
Ответ: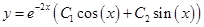
Пример 4.
Решить уравнение:
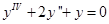
Составим и решим характеристическое уравнение
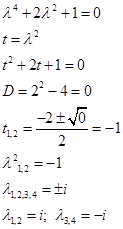
Получили две одинаковые парф комплексных сопряженных корней, т.е. кратности 2
, тогда общее решение однородного уравнения будет иметь вид:
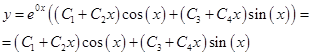
Ответ: 