Приведем полную формулировку теоремы Лапласа, взятую из учебника «Курс высшей алгебры» А.Г. Куроша.
Теорема Лапласа:
Пусть в определителе d порядка n произвольно выбраны k строк (или k столбцов),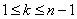 
. Тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d.
Напомним определения минора и алгебраического дополнения.
Определение:
Пусть в определителе d порядка n произвольно выбраны k строк и k столбцов, 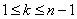. Элементы, стоящие на пересечении выбранных строк и столбцов представляют собой матрицу порядка k. Определитель этой матрицы и называется минором k-го порядка определителя d. Чаще всего обозначается буквой M.
Определение:
Дополнительным минором называется минор, полученный вычеркиванием из исходного определителя d строк и столбцов, составляющих минор M. Чаще всего обозначается M’.
Определение:
Алгебраическим дополнением минора M называется его дополнительный минор M’, взятый со знаком плюс, если сумма номеров всех строк и столбцов, в которых расположен минор M четна, и с минусом, если эта сумма нечетна.
Пример:
Рассмотрим определитель
Выберем первую, третью и четвертую строки и второй, третий и четвертый столбцы.
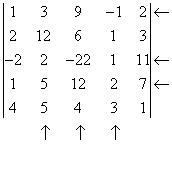
Составим определитель из элементов, стоящих на пересечениях этих строк и столбцов.
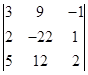.Это и будет минором 3-го порядка исходного определителя. Вычислим этот минор:
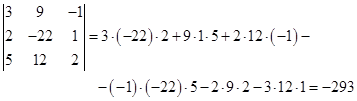
Итак, выбранный минор равен -293.
Дополнительным минором к нему будет определитель, составленный из элементов, стоящих на пересечении «оставшихся» строк и столбцов. В данном случае это первый и пятый столбцы и вторая и пятая строки.
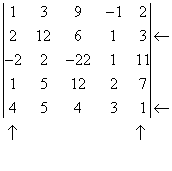
Получили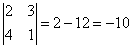 
. Это минор второго порядка, дополнительный с выбранному минору третьего порядка.
Для того, чтобы вычислить алгебраическое дополнение к выбранному минору третьего порядка осталось только выяснить знак, с которым следует взять дополнительный минор, т.е. -10.
Сложим все номера строк и столбцов.
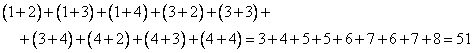
Получили нечетное число, значит дополнительный минор берется со знаком минус.
Т.о. алгебраическое дополнение к выбранному минору третьего порядка равно :
.
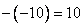Применим теорему Лапласа для вычисления определителя.
Пример:
Вычислить определитель
.
Применим теорему Лапласа.
1) «произвольно выбраны k строк» — выберем первую, третью и четвертую строки.
2) «Тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d.»
Один из миноров и его алгебраическое дополнение уже найдено выше:
Их произведение равно: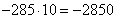 
.
Еще минор:
Его тоже нужно вычислить и умножить на его алгебраическое дополнение.
Всего миноров третьего порядка с элементами на первой, третьей и четвертой строках будет 10 штук. Конечно, их можно все вычислить, вычислить их алгебраические дополнения, перемножить попарно и сложить, получив в результате значение исходного определителя 5-го порядка, однако это достаточно трудоемкий процесс. О том, как рационально применять теорему Лапласа будет рассказано в следующей главе.