Назад Оглавление

Задача:
Найти плотность распределения частного двух независимых, равномернораспределенных на интервале 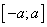случайных величин .

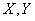Дано: 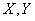— независимы.
,
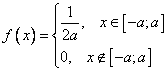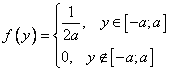
Найти функцию плотности распределения случайной величины .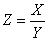
Решение:
Найдем двумерную функцию распределения.
Так как 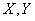— независимы, то 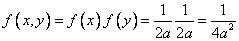при 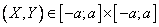. Вне этой области плотность равна нулю.
Найдем закон распределения величины 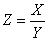. Для этого воспользуемся геометрической интерпретацией функции распределения, аналогичной функции одного аргумента. Но здесь будет уже не кривая, а поверхность.
Вообще говоря, если следовать логике, изложенной в предыдущем пункте статьи, то нужно построить поверхность 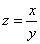, однако, значение функции будет неопределенно при 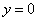, что затруднит построение в математических пакетах программ. Конечно, если человек может построить график аналитически, на бумажке, то никакой сложности нет. Здесь приведены два графика неявно заданной функции 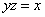. Поверхность представляет собой «архимедов винт», и, если брать пересечение этой поверхности плоскостью 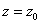, то в сечении будет прямая, являющаяся образующей этой поверхности, которая поворачивается, двигаясь вдоль оси аппликат.

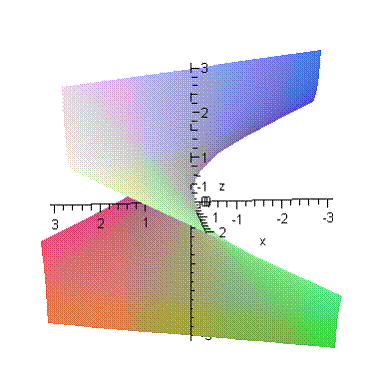
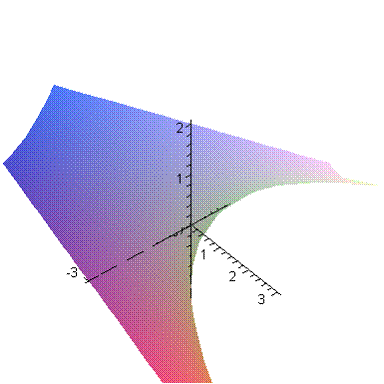
Не забудем, что функция определена на множестве:
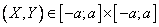
Перейдем к построению сечений на плоскости:
Зададимся некоторым значением 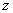(т.е. рассмотрим какое-то значение 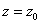) и построим на плоскости 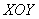прямую, уравнение которой: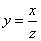
1) Рассмотрим случай

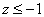
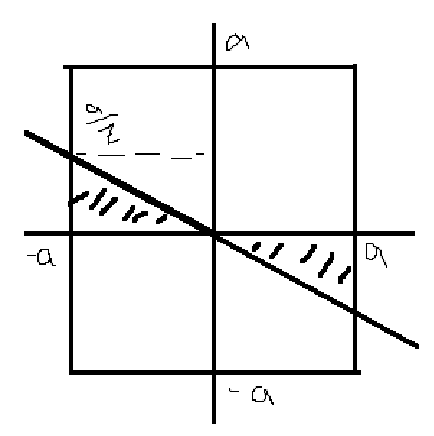
Заштрихованная область выбрана из соображения: 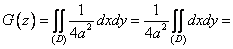, т.е. проекция той части «винта», которая будет лежать ниже плоскости сечения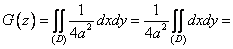

Этот интеграл равен площади области D, которая находится как площади двух треугольников:

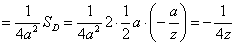
2) Рассмотрим случай
Область выглядит:


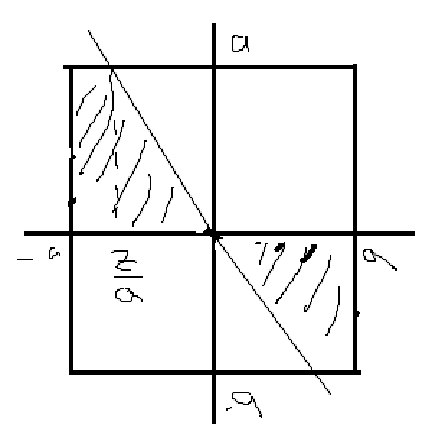
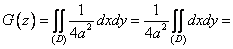
Аналогично находим как площадь:

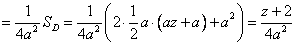
3) Рассмотрим случай
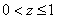
Область выглядит:


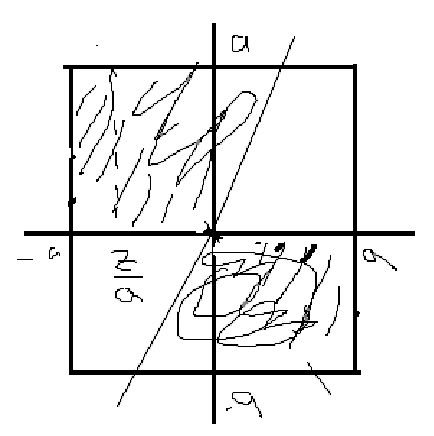
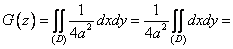
Аналогично находим как площадь:

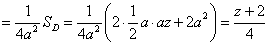
4) Рассмотрим случай
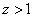
Область выглядит:


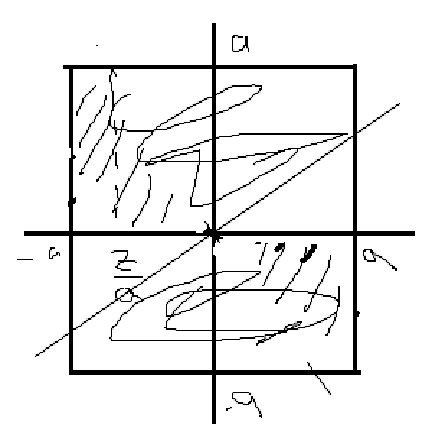
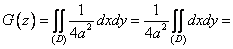
Опять находим как площадь фигуры:

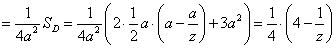
Составим функцию распределения:

Составим функцию плотности распределения:

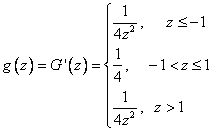
P.S. Статья создана при поддержке одного из читателей сайта.

Понравилась статья?

      Назад Оглавление