Итак, на предыдущей странице перечислены свойства, которыми обладает скалярное произведение. С помощью них можно доказать и вывести еще одну формулу для вычисления скалярного произведения и формулу для вычисления угла между векторами, координаты которых известны.
Формула для вычисления скалярного произведения векторов через их координаты.
Утверждение (Формула для вычисления скалярного произведения векторов): Для векторов, заданных своими координатами:
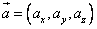и 
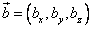
справедлива формула:
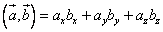.Произносится: Скалярное произведение векторов равно сумме произведений соответствующих координат.
Доказательство:
Запишем каждый вектор в виде разложения по базисным векторам:
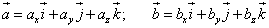
Запишем скалярное произведение:
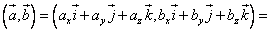
Используем свойство 7) :
Используем свойство 6):
Напомним, что
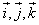— базисные вектора декартовой системы координат, т.е. они попарно перпендикулярны, значит, по свойству 2): 
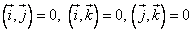.В итоге получим:
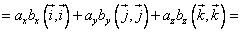
Последний шаг: по третьему свойству, зная, что
:
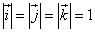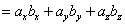.Замечание:
Для векторов на плоскости (двумерных) справедлива аналогичная формула, т.е. без последнего слагаемого:
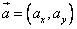и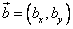 
: 
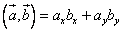.Формула для вычисления угла между векторами.
Замечание: Не столько угла, сколько косинуса угла.
Итак, на данный момент, для вычисления скалярного произведения есть:
а) определение:
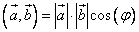,б) выведенная чуть ранее формула:
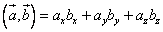.Выразим косинус угла между векторами из первого равенства:
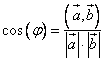
Произносится: косинус угла между векторами равен отношению скалярного произведения к произведению длин векторов.
А вычислить скалярное произведение можно про второй формуле. В результате получится вот такая формула (её и следует запомнить и применять для вычисления угла):
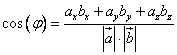.На следующей странице рассмотрим примеры решения задач с использование свойств и полученных формул.