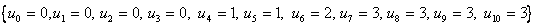На данный момент имеем контрольные точки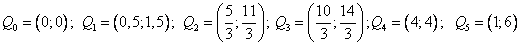 
Вектор узлов
В этом параграфе приведем пример разбиения построенной кривой на сплайны Безье. Это делается путем добавления узлов, причем одинаковых.
Предположим, что необходимо добавить контрольную точку, соответствующую узлу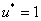 
(а такой уже имеется)
Это значение принадлежит интервалу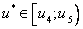 
.
Вычислим набор контрольных точек: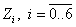 
.
Используем формулы:
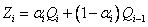
При этом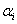 
определяются по формулам:
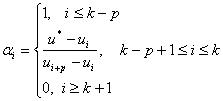
, где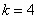 
— индекс нижней границы интервала, содержащего 
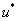, где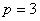 
— степень многочленов.
Начнем:
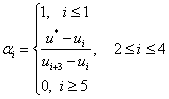
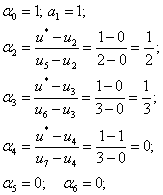
Теперь с точками:
Новый вектор узлов:
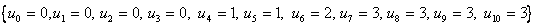
Новые контрольные точки
Первая строка
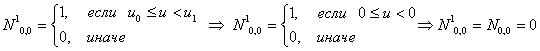
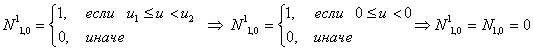
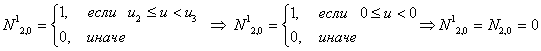
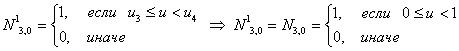
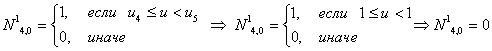
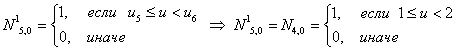
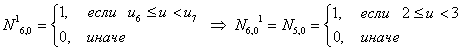
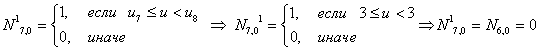
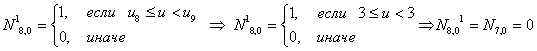
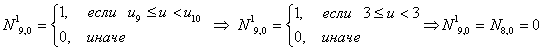
Итого, первая строка базисных функций для новых В-сплайнов:
Заметим, что первые четыре функции не изменились, пятая функция изменилась,
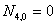как- бы «вклинилась», сдвинув остальные. В скобках показаны равные функции из предыдущего построения, откуда и будут браться их значения.
Из таблицы видно, что пересчитывать значения функций нужно только для тех, кто наследует от
:
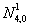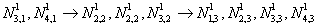
Вычислим функции, изменившие свои значения во второй строке
Третья строка
Последняя строка
Итого, базисные функции имеют вид (помним, что часть взята из предыдущего параграфа)
Составим функции:
Точки
Сплайн
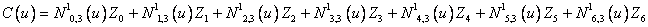
1) При значениях параметра: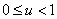 
2) При значениях параметра:
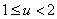
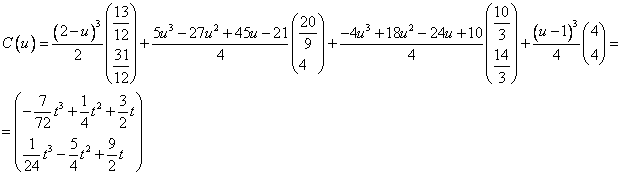
3) При значениях параметра:
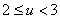
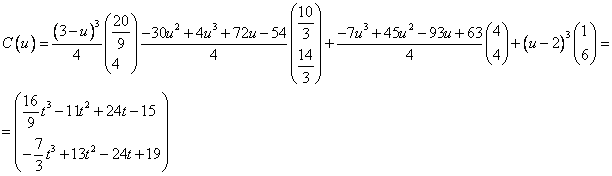
Вывод: Функции, описывающие сплайны, при добавлении узла, который уже есть в узловом векторе, не изменились.
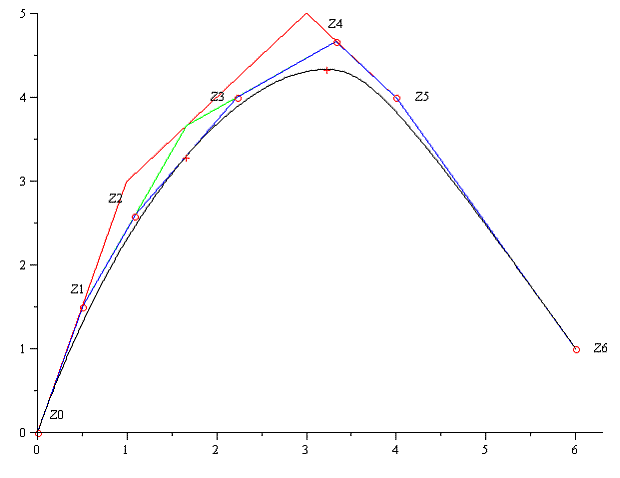
Замечание: На графике видно, что один из отрезков контрольного многоугольника касается. Наша цель, чтобы одна из контрольных точек принадлежала кривой. Для этого в вектор