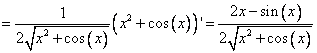Пример 1:
Вычислить производную функции 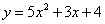
Решение:
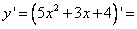
[Используем третье правило дифференцирования
 ]
]
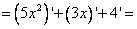
[ Для первого и второго слагаемого следуем применить четвертое правило дифференцирования 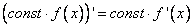 ]
]
[ для третьего слагаемого используем правило 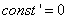 , для первого и второго -табличную производную
, для первого и второго -табличную производную 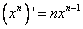 ]
]
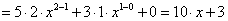
Пример 2:
Вычислить производную функции 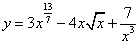
Решение:
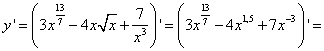
[Используем третье правило дифференцирования
 ]
]
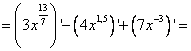
[Применим четвертое правило дифференцирования 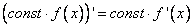 ]
]
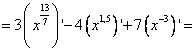
[Применим табличную производную
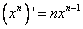 ]
]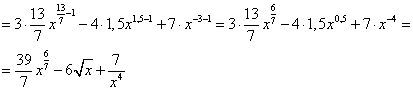
Пример 3:
Вычислить производную функции 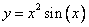
Решение:
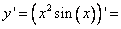
[Используем формулу дифференцирования произведения
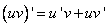 ]
]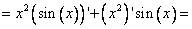
[Применим табличные производные 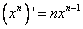 и
и 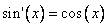 ]
]
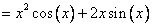
Пример 4:
Вычислить производную функции 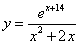
Решение:
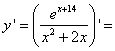
[Используем формулу дифференцирования частного
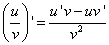 ]
]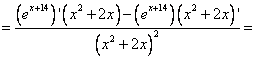
[ Все бы хорошо и по табличным производным. Кроме 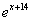 . Вспомним свойства степеней
. Вспомним свойства степеней 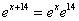 и вынесем константу за знак дифференциала.]
и вынесем константу за знак дифференциала.]

Производная сложной функции.
Формула: 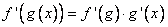
Её все равно никто не понимает, формулу эту, поэтому примеры:
Пример 5:
Вычислить производную функции 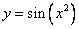
Решение:
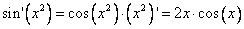
Пояснение: требуется вычислить производную функции синус от какого–то аргумента. Производная синуса равна косинусу. От того же аргумента (в данном случае это
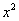 ). И умножим на производную аргумента.
). И умножим на производную аргумента.Можно даже сформулировать некое правило вычисления производной сложной функции
«Идти от наружной функции к внутренней».
Пример 6.
Вычислить производную функции
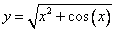
Решение:
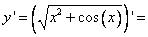
[Наружная функция это корень квадратный, помним, что
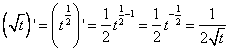 . Применим это, не забыв умножить на производную функции, стоящей внутри корня.]
. Применим это, не забыв умножить на производную функции, стоящей внутри корня.]