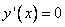 |
1. Точка подозрительная на экстремум. В этой точке функция может принимать максимальное или минимальное значение (а может и не принимать).
Если производная в этой точке меняет свой знак к «+» на «-», то это точка максимума. Если производная меняет свой знак с «-» на «+», то это точка минимума. 2. Производная равна нулю, значит в этой точке тангенс угла наклона касательной к графику функции равен нулю, т.е. касательная параллельна оси ОХ. |
 |
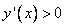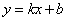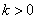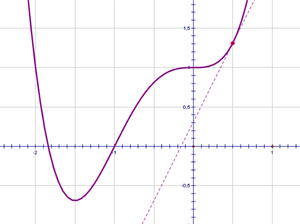1. Если на интервале  производная функции принимает положительные значения, то на этом интервале функция возрастает.2. Производная положительная, следовательно, тангенс угла наклона касательной положителен, значит в уравнении  , описывающем эту касательную, угловой коэффициент  . 3. В случае 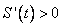 скорость точки положительна, т.е. идет движение «вперед».
|
 |
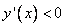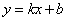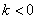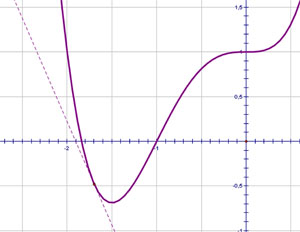1. Если на интервале производная функции принимает отрицательные значения, то на этом интервале функция убывает. 2. Производная отрицательна, следовательно, тангенс угла наклона касательной меньше нуля, значит в уравнении , описывающем эту касательную, угловой коэффициент  . 3. В случае 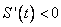 скорость точки отрицательна, т.е. идет движение «назад».
|
| Производная неопределена. |
В этой точке либо функция неопределена, либо график имеет излом. В задачах Единого Государственного Экзамена этот случай не встречается.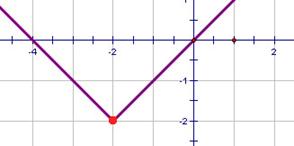
|
Главная > Самоучители > Подготовка к ЕГЭ-ГИА (элементарная математика) > Решение типовых заданий ЕГЭ по теме «Производные». > Основные факты, необходимые для решения типовых задач ЕГЭ с производными.
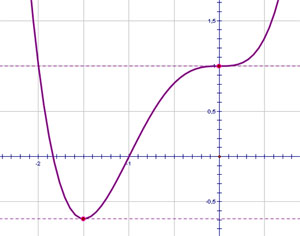
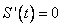скорость точки в момент времени 
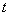равна нулю, т.е. точка стоит на месте.