Приведение к каноническому вижу уравнения математической физики ( уравнения в частных производных ) для функции трех переменных.
Задача: Привести к каноническому виду уравнение

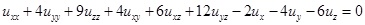
Решение:
Перенесем слагаемые первого порядка в правую часть равенства, они нас мало интересуют.

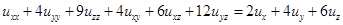
Поставим в соответствие левой части уравнения квадратичную форму и приведем её к каноническому виду.


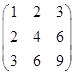
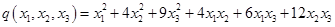
Выберем для приведения к каноническому виду метод Лагранжа.

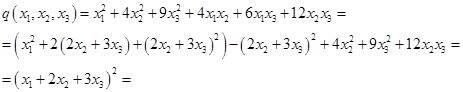
Сделаем замену:


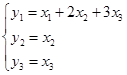
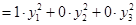
Тогда матрица перехода:
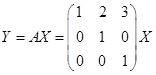, значит,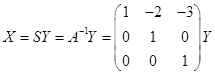
Замечание: если замен переменных будет несколько, то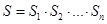
Получим канонический вид квадратичной формы:

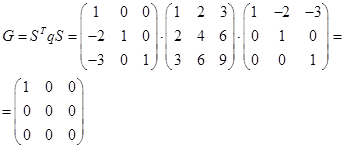
В результате должны были получить диагональную матрицу с 1,-1 или 0 на диагонали. Её и получили, диагональные элементы совпадают с коэффициентами при переменных, полученных методом Лагранжа, значит все хорошо.
Левая часть нашего исходного уравнения в частных производных примет вид:

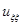
Для того, чтобы понять замену переменных, обратим внимание на столбцы матрицы S:

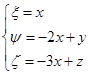
Определим, как видоизменится правая часть

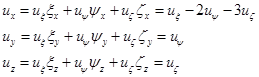
Подставим:

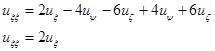
Получили уравнение гиперболического типа.