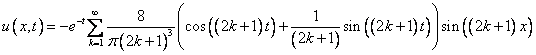Решить уравнение:
(
), 
, 
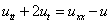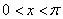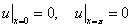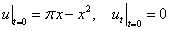
Решение:
Вид уравнения отличается от простейшего вида гиперболического уравнения, рассмотренного выше. Поэтому применим метод Фурье (метод разделения переменных) подробно. Это уравнения представляет собой уравнение свободных колебаний.
Решение будем искать в виде: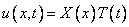 
, подставляем в исходное:
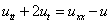
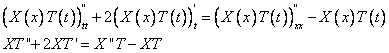
Поделим обе части уравнения на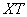 
.
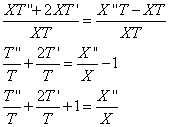
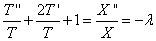
Получили два уравнения:
Рассмотрим первое из них:
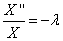
Решение этого уравнения при граничных условиях рассматривалось в первом параграфе:
, 
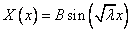, т.е., при 
, 
.
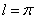
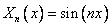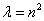Рассмотрим второе уравнение:
Известно, что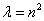
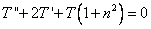
Получили дифференциальное уравнение, составим его характеристическое уравнение:
Следовательно, общее решение уравнения имеет вид:
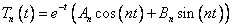
Вспомним, что решение ищется в виде 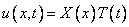и подставим сюда полученные выражения для функций:
.
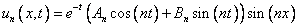Составляем ряд
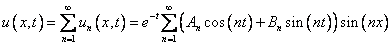, подберем коэффициенты так, чтобы выполнялись начальные условия.
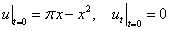
1) 
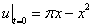
При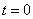 
:
Помним, что ищем коэффициенты разложения функции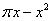 
в ряд Фурье по синусам. Они определяются по уже известной формуле:
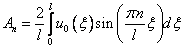
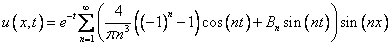
2)
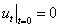
, возьмем производную по
.
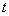Здесь можно не находить коэффициенты с помощью интегрирования, т.к. они должны быть равны 0.
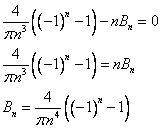
Итак, подставляем коэффициент:
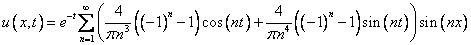
При четном
множитель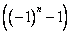 
обращается в ноль. Т.к. вычисляются решения, не равные тождественно нулю, то в ответ запишем лишь ненулевые слагаемые, т.е. при 
(нечетном).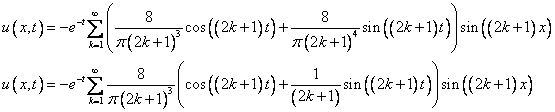
Ответ:
